Cho ΔABC vuông tại A, AB < AC. Phân giác BI. Đường cao AH. Trên BC lấy K sao cho BA = BK.
1. Chứng minh:
a) AI = IK
b) AH // IK
c) BI là trung trực AK
d) AK là phân giác góc HAC
2. Gọi AH giao BI tại N. Chứng minh:
a) Góc ANI = Góc AIN
b) NA = NK
c) NK ⊥ AB
3. Lấy E thuộc tia đối tia HA sao cho HA = HE. Chứng minh rằng: CB là phân giác góc ECA.
4. Kẻ KI giao AB tại D. Gọi V là trung điểm CD. Chứng minh:
a) ID = IC
b) B, I, V thẳng hàng
c) CD // AK
5. Kẻ IK giao CE tại M. Chứng minh:
a) CM = CI
b) CB là trung trực IM

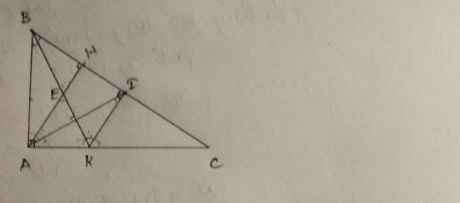
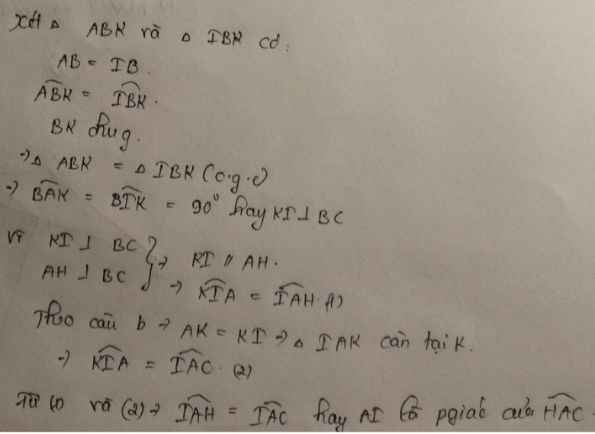
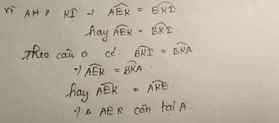
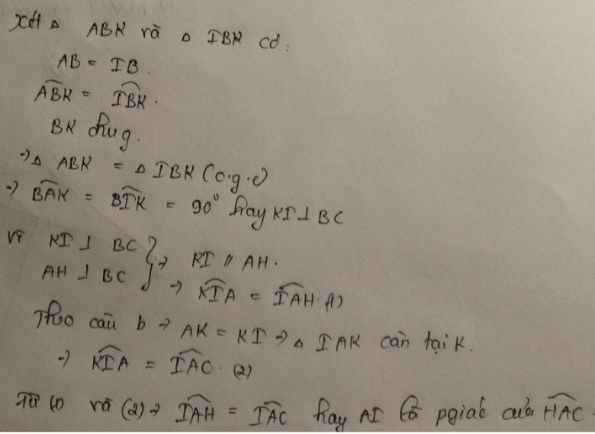
1:
a: Xét ΔBAI và ΔBKI có
BA=BK
\(\widehat{ABI}=\widehat{KBI}\)
BI chung
Do đó: ΔBAI=ΔBKI
=>IA=IK
b: ΔBAI=ΔBKI
=>\(\widehat{BAI}=\widehat{BKI}=90^0\)
=>IK\(\perp\)BC
mà AH\(\perp\)BC
nên AH//KI
c: BA=BK
=>B nằm trên đường trung trực của AK(1)
IA=IK
=>I nằm trên đường trung trực của AK(2)
Từ (1) và (2) suy ra BI là đường trung trực của AK
d: BA=BK
=>ΔBAK cân tại B
=>\(\widehat{BAK}=\widehat{BKA}\)
\(\widehat{BAK}+\widehat{CAK}=\widehat{BAC}=90^0\)
\(\widehat{BKA}+\widehat{HAK}=90^0\)(ΔKAH vuông tại H)
mà \(\widehat{BAK}=\widehat{BKA}\)
nên \(\widehat{CAK}=\widehat{HAK}\)
=>AK là phân giác của góc HAC
2:
a: Ta có: \(\widehat{ANI}=\widehat{BNH}\)(hai góc đối đỉnh)
\(\widehat{BNH}+\widehat{HBN}=90^0\)(ΔHNB vuông tại H)
Do đó: \(\widehat{ANI}+\widehat{HBN}=90^0\)
mà \(\widehat{HBN}=\widehat{ABI}\)
nên \(\widehat{ANI}+\widehat{ABI}=90^0\)
mà \(\widehat{ABI}+\widehat{AIN}=90^0\)(ΔABI vuông tại A)
nên \(\widehat{ANI}=\widehat{AIN}\)
b: Xét ΔBAN và ΔBKN có
BA=BK
\(\widehat{ABN}=\widehat{KBN}\)
BN chung
Do đó; ΔBAN=ΔBKN
=>NA=NK
c: BI là trung trực của AK
=>BI\(\perp\)AK
Xét ΔBAK có
BI,AH là đường cao
BI cắt AH tại N
Do đó: N là trực tâm của ΔBAK
=>KN\(\perp\)AB
3:
Xét ΔCAE có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAE cân tại C
=>CA=CE
ΔCAE cân tại C
mà CB là đường cao
nên CB là phân giác của \(\widehat{ACE}\)