Cho hình thang ABCD.Kẻ BK\(\perp\)AC.Lấy M,N lần lượt là trung điểm của AK,DC.Kẻ CI\(\perp\)BM(IB\(\in\)M) và CI cắt BK tại E.
a) C/m EB=EK b)C/m MNCE là hình bình hành
c)C/m MN\(\perp\)BM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MS
13 tháng 12 2023
a)Xét △BCM: \(\left\{{}\begin{matrix}CI\perp MB\\BK\perp MC\\CI\cap BK=E\end{matrix}\right.\)
Suy ra E là trực tâm của △BCM
\(\Rightarrow ME\perp BC\)
b) Theo kết quả của câu a: \(ME\perp BC\)
Mà \(AB\perp BC\) (Vì ABCD là hình chữ nhật)
=> ME//AB
Lại có M là trung điểm AK
=> E là trung điểm BK
=> ME là đường trung bình của △AKB
\(\Rightarrow\left\{{}\begin{matrix}ME//AB\\ME=\dfrac{1}{2}AB\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}ME//NC\\ME=NC\end{matrix}\right.\)
=> MNCE là hình bình hành
=> Đpcm
24 tháng 12 2023
a: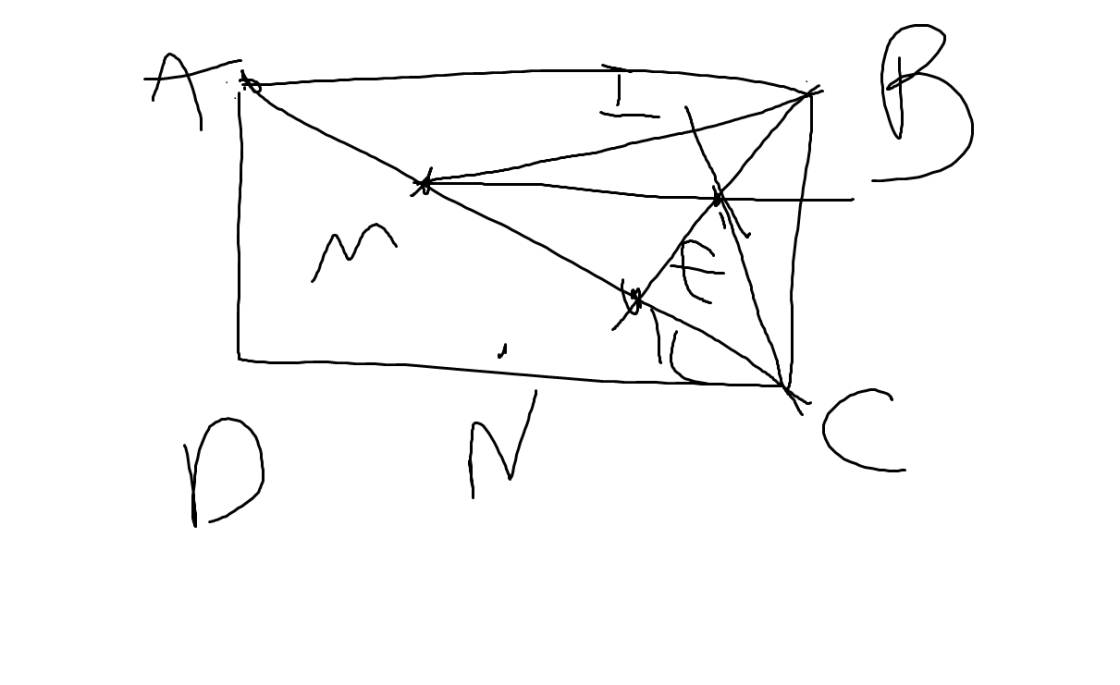 
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB
10 tháng 12 2021
a: Xét ΔACE có
CD là đường trung tuyến
CD là đường cao
CD=AE/2
Do đó: ΔACE vuông cân tại C
12 tháng 11 2023
Xét ΔBNC có
CI,BK là đường cao
CI cắt BK tại E
Do đó: E là trực tâm của ΔBNC
=>NE\(\perp\)BC
mà AB\(\perp\) BC
nên NE//AB
Xét ΔKAB có
N là trung điểm của KA
NE//AB
Do đó; E là trung điểm của BK
=>EB=EK