so sánh \(3^{19}\)và \(2^{30}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
LD
0

DT
1

LM
13 tháng 10 2021
\(\frac{19^{30}+5}{19^{31}+5}\)và \(\frac{19^{31}+5}{19^{32}+5}\)
Xét biểu thức \(\frac{19^{30}+5}{19^{31}+5}\)là A và biểu thức \(\frac{19^{31}+5}{19^{32}+5}\)là B
\(B=\frac{19^{31}+5}{19^{32}+5}< \frac{19^{31}+5+14}{19^{32}+5+14}\)
\(=\)\(\frac{19^{31}.19}{19^{32}.19}\)\(=\)\(\frac{19.\left(19^{30}+1\right)}{19.\left(19^{31}+1\right)}\)
\(=\)\(\frac{19^{30}+1}{19^{31}+1}\)
Mà \(\frac{19^{30}+1}{19^{31}+1}< \frac{19^{30}+5}{19^{31}+5}\)
Nên \(A>B\)
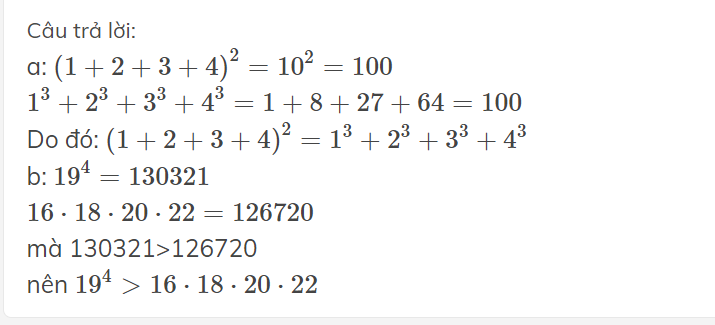
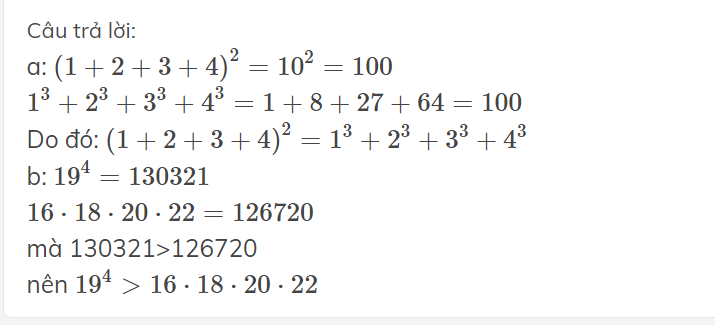
3^20 và 2^30 ( nghe còn có lý )
Ta có ; 3^20 = 3^2 . 10 = ( 3^2 ) ^ 10 = 9^10
2^30 = 2^3 . 10 = ( 2^3 ) ^ 10 = 8^10
Vì 8^10 < 9610
Nên 2^30 < 3^20
\(3^{19}>2^{30}\)