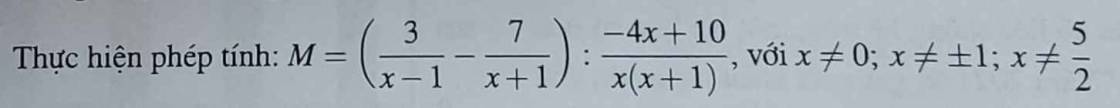 giúp mình câu này vs ạ
giúp mình câu này vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 13:
Ta có: \(f\left(x\right)>0\Leftrightarrow3x-m>0\Leftrightarrow3x>m\)
Mà x>1 hay 3x>3
Vậy \(m\le3\)
Đáp án C
Câu 14:
(d): x-2y+1=0 hay \(\dfrac{1}{2}x+\dfrac{1}{2}=y\)
Gọi phương trình đường thẳng cần tìm là: y=ax+b
Phương trình cần tìm đi qua A nên ta có: 2=-2a+b
Để phương trình cần tìm vuông góc với (d) thì: \(a.\dfrac{1}{2}=-1\Rightarrow a=-2\)\(\Rightarrow b=-2\)
Vậy phương trình cần tìm là: \(y=-2x-2\)
Đáp án C

b: \(=2\overrightarrow{IA}+2\overrightarrow{IM}=\overrightarrow{0}\)

Đặt \(\begin{cases} n_{Fe}=x(mol)\\ n_{Fe_2O_3}=y(mol)\\ n_{FeCO_3}=z(mol \end{cases} \Rightarrow 56x+160y+116c=30,4(1)\)
\(PTHH:Fe+2HCl\to FeCl_2+H_2\\ Fe_2O_3+6HCl\to 2FeCl_3+3H_2O\\ FeCO_3+2HCl\to FeCl_2+H_2O+CO_2\uparrow\\ M_{\text{hh khí}}=15.2=30(g/mol)\\ \Rightarrow \dfrac{m_{H_2}+m_{CO_2}}{n_{H_2}+n_{CO_2}}=30\\ \Rightarrow \dfrac{2x+44z}{x+z}=30\\ \Rightarrow 28x-14z=0(2)\)
\(m_{muối}=m_{FeCl_2}+m_{FeCl_3}=51,55\\ \Rightarrow 127(x+z)+162,5.2y=51,55\\ \Rightarrow 127x+325y+127z=51,55(3)\\ (1)(2)(3)\Rightarrow \begin{cases} x=0,05(mol)\\ y=z=0,1(mol) \end{cases} \\ \Rightarrow \begin{cases} \%_{Fe}=\dfrac{0,05.56}{30,4}.100\%=9,21\%\\ \%_{Fe_2O_3}=\dfrac{0,1.160}{30,4}.100\%=52,63\%\\ \%_{FeCO_3}=100\%-9,21\%-52,63\%=38,16\%\\ \end{cases}\\ b,\Sigma n_{HCl}=2x+6y+2z=0,9(mol)\\ \Rightarrow C_{M_{HCl}}=\dfrac{0,9}{1,8}=0,5M\)

1. How much money do you need?
2. How many languages can she speak?
3. How many kilos of rice do you need?
4. How many meals does he have a day?
5. How much milk and coffe do they need?
6. How many oranges and apples would you like?
7. How much sugar is there in the cup?
8. How many glasses of beer can he drink?
9. How much do this books cost?
10. How many kilos of rice and eggs do you need?


Áp dụng hệ thức lượng:
\(AH^2=BH.CH=4.9=36\)
\(\Rightarrow AH=6\left(cm\right)\)
\(BC=4+9=13\left(cm\right)\)
- Nếu \(BH=4\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Rightarrow AB=\sqrt{4.13}=2\sqrt{13}\) (cm)
\(sinC=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{13}\Rightarrow C\approx33^041'\)
- Nếu \(BH=9\Rightarrow AB=\sqrt{BH.BC}=\sqrt{9.13}=3\sqrt{13}\left(cm\right)\)
\(sinC=\dfrac{AB}{BC}=\dfrac{3\sqrt{13}}{13}\Rightarrow C\approx56^019'\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.6.13=39\left(cm^2\right)\)
(Vì đề không nói rõ BH, CH bằng 4 hay 9 nên mình cho BH = 4 và CH = 9 nhé!)
Áp dụng HTL vào \(\Delta ABC\) vuông tại A đường cao AH:
\(AH^2=BH\cdot HC\Leftrightarrow AH=\sqrt{BH\cdot HC}=\sqrt{4\cdot9}=6\left(cm\right)\)
Áp dụng HTL vào \(\Delta ABH\) vuông tại H:
\(AB^2=AH^2+BH^2\Leftrightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
Áp dụng tslg vào \(\Delta ABC\) vuông tại A, đường cao AH:
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{4+9}\approx34^0\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot2\sqrt{13}\cdot\left(\sqrt{13^2-\left(2\sqrt{13}\right)^2}\right)_{Pytago}=39cm^2\)











Với \(x\ne0;x\ne\pm1;x\ne\dfrac{5}{2}\), ta có:
\(M=\left(\dfrac{3}{x-1}-\dfrac{7}{x+1}\right):\dfrac{-4x+10}{x\left(x+1\right)}\)
\(=\left[\dfrac{3\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}-\dfrac{7\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)
\(=\dfrac{3x+3-7x+7}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x\left(x+1\right)}{-4x+10}\)
\(=\dfrac{-4x+10}{x-1}\cdot\dfrac{x}{-4x+10}\)
\(=\dfrac{x}{x-1}\)
\(Toru\)