Cho tam giác ABC nhọn.Đường tròn tâm O đường kính BC cắt AB ở M và cắt AC ở N.Gọi H là gia điểm của BN và CMA.Chứng minh AH vuông góc với BC.B. Gọi E là trung điểm AH.Chứng minh bốn điểm A,M,H,E cùng nằm trên một đường tròn và EM là tiếp tuyến của đường tròn(O)c.chứng minh MN,OE=2ME.MOD.giả sử AH=BC.Tính tan...
Đọc tiếp
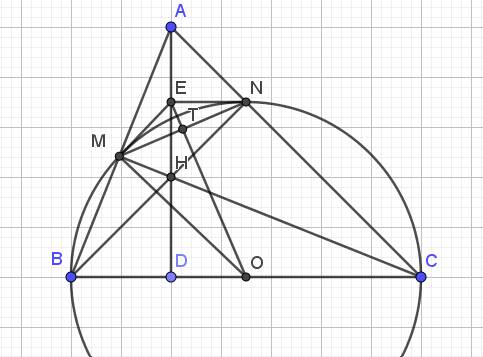
Cho tam giác ABC nhọn.Đường tròn tâm O đường kính BC cắt AB ở M và cắt AC ở N.Gọi H là gia điểm của BN và CM
A.Chứng minh AH vuông góc với BC.
B. Gọi E là trung điểm AH.Chứng minh bốn điểm A,M,H,E cùng nằm trên một đường tròn và EM là tiếp tuyến của đường tròn(O)
c.chứng minh MN,OE=2ME.MO
D.giả sử AH=BC.Tính tan BAC
a: Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó:ΔBMC vuông tại M
=>BM\(\perp\)MC tại M
=>CM\(\perp\)AB tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
Do đó: ΔBNC vuông tại N
=>BN\(\perp\)NC tại N
=>BN\(\perp\)AC tại N
Xét ΔABC có
BN,CM là đường cao
BN cắt CM tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
b: Xét tứ giác AMHN có \(\widehat{AMH}+\widehat{ANH}=90^0+90^0=180^0\)
nên AMHN là tứ giác nội tiếp đường tròn đường kính AH
=>A,M,H,N cùng thuộc (E)
Gọi giao điểm của AH với BC là F
Xét ΔABC có
H là trực tâm của ΔABC
F là giao điểm của AH với BC
Do đó: AH\(\perp\)BC tại F
=>ΔAFB vuông tại F
=>\(\widehat{ABF}+\widehat{BAF}=90^0\)
mà \(\widehat{ABF}+\widehat{MCB}=90^0\)(ΔCMB vuông tại M)
nên \(\widehat{BAF}=\widehat{MCB}\)
\(\widehat{EMO}=\widehat{EMH}+\widehat{OMH}\)
=\(\widehat{EHM}+\widehat{OCM}\)
\(=90^0-\widehat{MAH}+\widehat{MCB}\)
\(=90^0\)
=>EM là tiếp tuyến của (O)