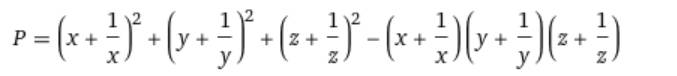cho xyz=1 tính giá trị biểu thức P
mình cần gấp, giúp mình vs ạ. Mình cảm ơn!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
T
0
Những câu hỏi liên quan
T
1
H9
HT.Phong (9A5)
CTVHS
23 tháng 11 2023
\(P=\left(x+\dfrac{1}{x}\right)^2+\left(y+\dfrac{1}{y}\right)^2+\left(z+\dfrac{1}{z}\right)^2-\left(x+\dfrac{1}{x}\right)\left(y+\dfrac{1}{y}\right)\left(z+\dfrac{1}{z}\right)\)
Ta có: \(xyz=1\Rightarrow x=\dfrac{1}{yz}\)
\(P=\left(\dfrac{1}{yz}+yz\right)^2+\left(y+\dfrac{1}{y}\right)^2+\left(z+\dfrac{1}{z}\right)^2-\left(yz+\dfrac{1}{yz}\right)\left(y+\dfrac{1}{y}\right)\left(z+\dfrac{1}{z}\right)\)
\(P=\dfrac{1}{y^2z^2}+2+1y^2z^2+y^2+2+\dfrac{1}{y^2}+z^2+2+\dfrac{1}{z^2}-\left(y^2z+z+\dfrac{1}{z}+\dfrac{1}{y^2z}\right)\left(z+\dfrac{1}{z}\right)\)
\(P=\dfrac{1}{y^2z^2}+y^2z^2+y^2+\dfrac{1}{y^2}+z^2+\dfrac{1}{z^2}+6-y^2z^2-y^2-z^2-1-1-\dfrac{1}{z^2}-\dfrac{1}{y^2}-\dfrac{1}{y^2z^2}\)\(P=\left(\dfrac{1}{y^2z^2}-\dfrac{1}{y^2z^2}\right)+\left(y^2z^2-y^2z^2\right)+\left(y^2-y^2\right)+\left(z^2-z^2\right)+\left(\dfrac{1}{y^2}-\dfrac{1}{y^2}\right)+\left(\dfrac{1}{z^2}-\dfrac{1}{z^2}\right)+4\)
\(P=4\)
Vậy: ...
DD
2
4 tháng 7 2018
\(a,P=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
\(=\left(x^2+5x+5-1\right)\left(x^2+5x+5+1\right)+1\)
\(=\left(x^2+5x+5\right)^2-1+1\)
\(=\left(x^2+5x+5\right)^2\ge0\forall x\)
Vậy \(P\ge0\forall x\)
\(b,P=\left(x^2+5x+5\right)^2\left(cmt\right)\)
Thay \(x=\frac{\sqrt{7}-5}{2}\)vào P ta được
\(P=\left(\left(\frac{\sqrt{7}-5}{2}\right)^2+5.\frac{\sqrt{7}-5}{2}+5\right)^2\)
\(=\left(\frac{7-10\sqrt{7}+25}{4}+\frac{10\sqrt{7}-50}{4}+\frac{20}{4}\right)^2\)
\(=\left(\frac{32-10\sqrt{7}+10\sqrt{7}-50+20}{4}\right)^2\)
\(=\left(\frac{2}{4}\right)^2\)
\(=\frac{1}{4}\)
4 tháng 7 2018
a,
P=(x+1)(x+2)(x+3)(x+4)+1
P=[(x+1).(x+4)].[(x+2).(x+3)]+1
P=(x^2+5x+4)(x^2+5x+6)+1
P=[(x^2+5x+5)-1].[(x^2+5x+5)+1]+1
P=(x^2+5x+5)^2-1+1
P=\(\left(x^2+5x+5\right)^2\) \(\ge\)0 với mọi x
Câu b thì thay x vào rồi bấm máy ra ra kết quả
12 tháng 7 2021
Bài 2:
a) Ta có: \(\left|2x-5\right|\ge0\forall x\)
\(\Leftrightarrow-\left|2x-5\right|\le0\forall x\)
\(\Leftrightarrow-\left|2x-5\right|+3\le3\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)
16 tháng 7 2019
Vì \(x=2017\Rightarrow x+1=2018\)
Thay \(x+1=2018\)vào biểu thức A ta được :
\(A=x^{10}-\left(x+1\right)x^9+\left(x+1\right)x^8-...-\left(x+1\right)x+\left(x+1\right)\)
\(=x^{10}-x^{10}-x^9+x^9+x^8-...-x^2-x+x+1\)
\(=1\)
10 tháng 3 2020
- Ta có: \(x+y+z=0\)
\(\Leftrightarrow x+y=-z\)
\(\Leftrightarrow\left(x+y\right)^2=\left(-z\right)^2\)
\(\Leftrightarrow x^2+y^2+2xy=z^2\)
\(\Leftrightarrow x^2+y^2-z^2=-2xy\)
- CMT2: \(y^2+z^2-x^2=-2yz\)
\(z^2+x^2-y^2=-2zx\)
- Thay \(x^2+y^2-z^2=-2xy,\)\(y^2+z^2-x^2=-2yz,\)\(z^2+x^2-y^2=-2zx\)vào đa thức P
- Ta có: \(P=\frac{x^2}{-2yz}+\frac{y^2}{-2zx}+\frac{z^2}{-2xy}\)
\(\Leftrightarrow P=\frac{x^3+y^3+z^3}{-2xyz}\)
- Đặt \(a=x^3+y^3+z^3\)
- Ta lại có: \(a=\left(x+y\right)^3+z^3-3xy.\left(x+y\right)\)
\(\Leftrightarrow a=\left(x+y+z\right)^3-3.\left(x+y\right).z.\left(x+y+z\right)-3ab.\left(x+y\right)\)
- Mặt khác: \(x+y+z=0\)
\(\Leftrightarrow x+y=-z\)
- Thay \(x+y+z=0,\)\(x+y=-z\)vào đa thức a
- Ta có: \(a=-3xy.\left(-z\right)=3xyz\)
- Thay \(a=3xyz\)vào đa thức P
- Ta có: \(P=\frac{3xyz}{-2xyz}=-\frac{3}{2}\)
Vậy \(P=-\frac{3}{2}\)
AH
Akai Haruma
Giáo viên
9 tháng 10 2023
Lời giải:
Vì $x=9$ nên $x-9=0$
Ta có:
$F=(x^{2017}-9x^{2016})-(x^{2016}-9x^{2015})+(x^{2015}-9x^{2014})-....-(x^2-9x)+x-10$
$=x^{2016}(x-9)-x^{2015}(x-9)+x^{2014}(x-9)-....-x(x-9)+x-10$
$=x^{2016}.0-x^{2015}.0+x^{2014}.0-...-x.0+x-10$
$=x-10=9-10=-1$
20 tháng 11 2017
15,46 + 20,09 + 11,3+ 4,18
=35,55+11,3+4,18
=46,85+4,18
=51,03