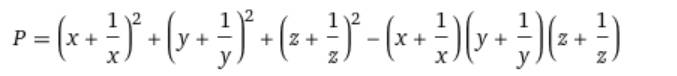cho xyz=1. Tính giá trị của biểu thức trên
giúp mik vs ạ! mình xin cảm ơn!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
T
1
Những câu hỏi liên quan
8 tháng 3 2022
a: \(B=\left(\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x-2}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(=\dfrac{x-2x-4+x-2}{\left(x-2\right)\left(x+2\right)}:\dfrac{x^2-4+10-x^2}{x+2}\)
\(=\dfrac{-6}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x+2}{6}=\dfrac{-1}{x-2}\)
b: Khi x=1/2 thì \(B=\dfrac{-1}{\dfrac{1}{2}-2}=\dfrac{2}{3}\)
Khi x=-1/2 thì B=2/5
c: Để B nguyên thì \(x-2\in\left\{1;-1\right\}\)
hay \(x\in\left\{3;1\right\}\)
8 tháng 3 2022
a, đk : x khác -2 ; 2
\(B=\left(\dfrac{x-2\left(x+2\right)+x-2}{\left(x-2\right)\left(x+2\right)}\right):\left(\dfrac{x^2-4+10-x^2}{x+2}\right)\)
\(=\dfrac{-6}{\left(x-2\right)\left(x+2\right)}:\dfrac{6}{x+2}=\dfrac{1}{2-x}\)
b, Ta có \(\left|x\right|=\dfrac{1}{2}\Leftrightarrow x=\dfrac{1}{2};x=-\dfrac{1}{2}\)
Với x = 1/2 ta được \(B=\dfrac{1}{2-\dfrac{1}{2}}=\dfrac{2}{3}\)
Với x = -1/2 ta được \(B=\dfrac{1}{2+\dfrac{1}{2}}=\dfrac{2}{5}\)
c, \(\dfrac{1}{2-x}\Rightarrow2-x\inƯ\left(1\right)=\left\{\pm1\right\}\)
| 2-x | 1 | -1 |
| x | 1 | 3 |
13 tháng 2 2019
Để \(A=\frac{2x^2+3x+3}{2x+1}\)nguyên thì :
\(\left(2x^2+3x+3\right)⋮\left(2x+1\right)\)
\(\left(2x^2+x+2x+1+2\right)⋮\left(2x+1\right)\)
\(\left[x\left(2x+1\right)+\left(2x+1\right)+2\right]⋮\left(2x+1\right)\)
\(\left[\left(2x+1\right)\left(x+1\right)+2\right]⋮\left(2x+1\right)\)
Vì \(\left(2x+1\right)\left(x+1\right)⋮\left(2x+1\right)\)
\(\Rightarrow2⋮\left(2x+1\right)\)
\(\Rightarrow2x+1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow x\in\left\{0;-1;0,5;-1,5\right\}\)
Vậy....
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
\(A=\dfrac{5x^2}{x^2}-\dfrac{x}{x^2}+\dfrac{1}{x^2}=\dfrac{1}{x^2}-\dfrac{1}{x}+5=\left(\dfrac{1}{x^2}-\dfrac{1}{x}+\dfrac{1}{4}\right)+\dfrac{19}{4}=\left(\dfrac{1}{x}-\dfrac{1}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\)
\(A_{min}=\dfrac{19}{4}\) khi \(\dfrac{1}{x}=\dfrac{1}{2}\Rightarrow x=2\)
13 tháng 12 2017
Tiếp tục:\(-A=\frac{x^3+y^3+z^3}{2xyz}\)
thay(1) vào A ta có
\(-A=\frac{y^3+z^3-\left(y+z\right)^3}{2xyz}=\frac{y^3+z^3-y^3-z^3-3yz\left(y+z\right)}{2xyz}\)
\(-A=\frac{3xyz}{2xyz}=\frac{3}{2}\Rightarrow A=\frac{-3}{2}\)
P/s tham khảo bài mình nhé nhớ
13 tháng 12 2017
ta có:\(x+y+z=0\) \(\Rightarrow x=-\left(y+z\right)\)
\(\Rightarrow x^3=-\left(y+z\right)^3\left(1\right)\)\(;x^2=\left(y+z\right)^2\)
\(\Rightarrow y^2+z^2-x^2=-2yz\)
CMTT:\(z^2+x^2-y^2=-2xz;x^2+y^2-z^2=-2xy\)
thay vào A ta có:
\(A=\frac{-x^2}{2yz}+\frac{-y^2}{2xz}+\frac{-z^2}{2xy}\)
\(P=\left(x+\dfrac{1}{x}\right)^2+\left(y+\dfrac{1}{y}\right)^2+\left(z+\dfrac{1}{z}\right)^2-\left(x+\dfrac{1}{x}\right)\left(y+\dfrac{1}{y}\right)\left(z+\dfrac{1}{z}\right)\)
Ta có: \(xyz=1\Rightarrow x=\dfrac{1}{yz}\)
\(P=\left(\dfrac{1}{yz}+yz\right)^2+\left(y+\dfrac{1}{y}\right)^2+\left(z+\dfrac{1}{z}\right)^2-\left(yz+\dfrac{1}{yz}\right)\left(y+\dfrac{1}{y}\right)\left(z+\dfrac{1}{z}\right)\)
\(P=\dfrac{1}{y^2z^2}+2+1y^2z^2+y^2+2+\dfrac{1}{y^2}+z^2+2+\dfrac{1}{z^2}-\left(y^2z+z+\dfrac{1}{z}+\dfrac{1}{y^2z}\right)\left(z+\dfrac{1}{z}\right)\)
\(P=\dfrac{1}{y^2z^2}+y^2z^2+y^2+\dfrac{1}{y^2}+z^2+\dfrac{1}{z^2}+6-y^2z^2-y^2-z^2-1-1-\dfrac{1}{z^2}-\dfrac{1}{y^2}-\dfrac{1}{y^2z^2}\)\(P=\left(\dfrac{1}{y^2z^2}-\dfrac{1}{y^2z^2}\right)+\left(y^2z^2-y^2z^2\right)+\left(y^2-y^2\right)+\left(z^2-z^2\right)+\left(\dfrac{1}{y^2}-\dfrac{1}{y^2}\right)+\left(\dfrac{1}{z^2}-\dfrac{1}{z^2}\right)+4\)
\(P=4\)
Vậy: ...