làm giúp em bài 4 với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 10 2021
3: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}\)
\(\Leftrightarrow AB=12.5\left(cm\right)\)
\(\Leftrightarrow AC=12.5\sqrt{3}\left(cm\right)\)
HT
3
NN
22 tháng 4 2021
a) Ta có: AB//CD.
=>ABH=BDC (2 góc so le trong).
=> ∆AHB~∆BCD(g.g).
b) ∆ABD có : DB²=AB²+AD²( Định lý Pitago)
=> DB= 15(cm).
Ta có ∆ABH~∆BCD(cmt).
=>AH/BC=AD/BD.
Hay AH=9.12/15=7,2(cm).
c)Ta có ∆AHB~∆BCD cmt.
=> HBA=CBD. (1)
Ta lại có : CBD= ADH (AB//CD).(2)
Từ 1 và 2 => HAB=ADH.
=>∆DHA~∆AHB(g.g).
S∆DHA/S∆AHB=(AD/AB)²=9/16
d) từ câu (a) và (b) => ∆BCD~∆DHA.
Cm ∆DHA~∆MDA(g.g)
Từ đó suy ra ∆BDC~∆MDA.
Sau đó cm ∆BCD~∆ADC(g.g).
=> ∆MDA~∆ADC(g.g).
=>Ad/DC=DM/DC.
=>Đpcm.
3 tháng 10 2021
câu 4:
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\)
hay AH=6(cm)
b: Xét ΔBAC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
nên \(AM=\dfrac{BC}{2}=6.5\left(cm\right)\)
7 tháng 10 2021
Câu 4:
\(x^6-1=\left(x^2-1\right)\left(x^4+x^2+1\right)⋮x^4+x^2+1\)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 8 2021
Với 2 số thực bất kì \(x_1;x_2\) sao cho \(x_1< x_2\) ta có:
\(f\left(x_1\right)-f\left(x_2\right)=-x_1^3+x_1^2-x_1+5-\left(-x_2^3+x_2^2-x_2+5\right)\)
\(=x_2^3-x_1^3+x_1^2-x_2^2-x_1+x_2\)
\(=\left(x_2-x_1\right)\left(x_1^2+x_2^2+x_1x_2\right)-\left(x_2-x_1\right)\left(x_1+x_2\right)+x_2-x_1\)
\(=\left(x_2-x_1\right)\left(x_1^2+x_2^2+x_1x_2-x_1-x_2+1\right)\)
\(=\left(x_2-x_1\right)\left[\left(x_1+\dfrac{x_2}{2}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}x_2^2-\dfrac{1}{2}x_2+\dfrac{3}{4}\right]\)
\(=\left(x_2-x_1\right)\left[\left(x_1+\dfrac{x_2}{2}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\left(x_2-\dfrac{1}{3}\right)^2+\dfrac{2}{3}\right]>0\)
\(\Rightarrow f\left(x_1\right)>f\left(x_2\right)\Rightarrow\) hàm nghịch biến trên R
NM
1
BN
3
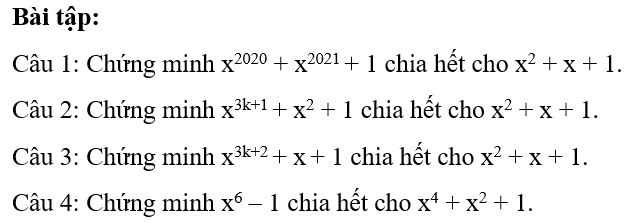
a: Xét (O) có
CA,CM là tiếp tuyến
Do đó: CA=CM và OC là phân giác của \(\widehat{MOA}\)
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là tiếp tuyến
Do đó: DM=DB và OD là phân giác của \(\widehat{MOB}\)
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
\(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOD}+2\cdot\widehat{MOC}=180^0\)
=>\(2\cdot\left(\widehat{MOD}+\widehat{MOC}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
=>ΔOCD vuông tại O
b: Xét ΔOCD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2=R^2\)
c: ΔOAC vuông tại A
=>\(OA^2+AC^2=OC^2\)
=>\(CA^2+R^2=\left(2R\right)^2=4R^2\)
=>\(CA^2=3R^2\)
=>\(CA=R\sqrt{3}\)
\(AC\cdot BD=MA\cdot MD=R^2\)
=>\(BD\cdot R\sqrt{3}=R^2\)
=>\(BD=\dfrac{R^2}{R\sqrt{3}}=\dfrac{R}{\sqrt{3}}\)