Tổng của 2 số bằng 59. Hai lần của số này bé hơn 3 lần của số kia là 7. Tìm 2 số đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 3 2017
Gọi x, y là hai số cần tìm.
Vì tổng của hai số bằng 59 nên ta có phương trình: x + y = 59
Vì hai lần của số này bé hơn ba lần của số kia là 7 nên ta có phương trình: 3y – 2x = 7.
Ta có hệ phương trình: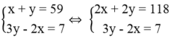 
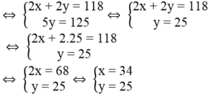
Vậy hai số cần tìm là 34 và 25
TP
31 tháng 5 2017
tuyết mây
Gọi hai số cần tìm là a và b. Theo đề bài, ta có:
a+b=59 → 3a+3b=177
Vậy: (3a+3b)−(3b−2a)=170 → a=34. Vậy, b=25
31 tháng 5 2017
gọi số bé là x
số lớn là 59 - x
vì 2 lần số này bé hơn 3 lần số kia 7 đơn vị nên :
\(3.x-2\left(59-x\right)=7\Leftrightarrow5x=125\Leftrightarrow x=25\)
vậy số bé là 25
số lớn là 59-25 =34
QQ
1
15 tháng 1 2023
Tổng hai số = 59
=> x + y = 59 (1)
2 lần số này bé hơn 3 lần số kia là 57
=> -2x + 3y = 57 (2)
Từ (1) và (2) ta được hệ phương trình:
{x + y = 59
{-2x + 3y = 57
<=> {x = 24
{y = 35
12 tháng 7 2017
Gọi số bé là a;số lớn là b
Tổng 2 số là 59 \(\Rightarrow a+b=59\)
Hai lần số lớn bé hơn 3 lần số bé là 7 \(\Rightarrow3a-2b=7\)
Thay \(a=59-b\Rightarrow3\left(59-b\right)-2b=7\Rightarrow-5b=-170\Rightarrow b=34\)
\(\Rightarrow a=25\)
Vậy số lớn là 34 , só bé là 25
12 tháng 7 2017
gọi số lớn , bé ll là a,b (a,b>0)
theo đề bài ta có a+b=59
3a-2b=7
giải hệ pt ta dược a=25 b=34
CM
17 tháng 2 2018
Gọi 2 số cần tìm là x; y.
Tổng của 2 số là 59 nên ta có: x + y = 54
Ba lần số này hơn số kia là 2 nên: 3x – y =2
Ta có hệ phương trình:
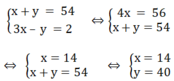
Vậy hai số cần tìm là 14 và 40.
DX
1
GH
27 tháng 6 2023
Gọi x, y là 2 số đó.
Tổng của hai số bằng 23, ta có:
x + y = 23 (1)
2 lần số này lớn hơn số kia 1 đơn vị, ta có:
2x - y = 1 (2)
Từ (1), (2) có hệ phương trình: \(\left\{{}\begin{matrix}x+y=23\\2x-y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=46\\2x-y=1\end{matrix}\right.\\ \Leftrightarrow3y=45\\ \Rightarrow y=15\Rightarrow x=\dfrac{1+15}{2}=8\)
Vậy 2 số đó là 15 và 8
HN
1
20 tháng 12 2016
Gọi 2 số cần tìm lần lượt là x; y (x; y >0)
Ta có:
x + y = 15
3x = 2y => \(\frac{x}{2}=\frac{y}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{x+y}{2+3}=\frac{15}{5}=3\)
=> \(\frac{x}{2}=3=>x=3.2=6\)
\(\frac{y}{3}=3=>y=3.3=9\)
Vậy 2 số cần tìm là 6 và 9
Gọi hai số cần tìm là a,b
Tổng của hai số là 59 nên a+b=59(1)
Hai lần của số này bé hơn 3lần của số kia là 7 nên ta có:
3a-2b=7(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=59\\3a-2b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+2b=118\\3a-2b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5a=125\\a+b=59\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=25\\b=59-a=59-25=34\end{matrix}\right.\)
Vậy: Hai số cần tìm là 25 và 34