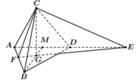
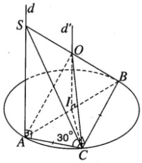
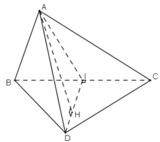
Cho tứ diện A1A2A3A4. Xét 6 mặt phẳng, mỗi mặt phẳng đi qua trung điểm của một cạnh và vuông góc với cạnh đối diện.
a) Chứng minh rằng 6 mặt phẳng này cùng đi qua một điểm M. (Điểm này được gọi là điểm "Monge" của hình tứ diện A1A2A3A4)
b) CMR \(\left\{{}\begin{matrix}\overrightarrow{MA_1}.\overrightarrow{MA_2}=\overrightarrow{MA_3}.\overrightarrow{MA_4}\\\overrightarrow{MA_1}.\overrightarrow{MA_3}=\overrightarrow{MA_2}.\overrightarrow{MA_4}\\\overrightarrow{MA_1}.\overrightarrow{MA_4}=\overrightarrow{MA_2}.\overrightarrow{MA_3}\end{matrix}\right.\)
c) Giả sử M nằm trện một mặt bất kì của tứ diện. CMR chân đường cao ứng với mặt đó nằm trên đường tròn ngoại tiếp của mặt đó.