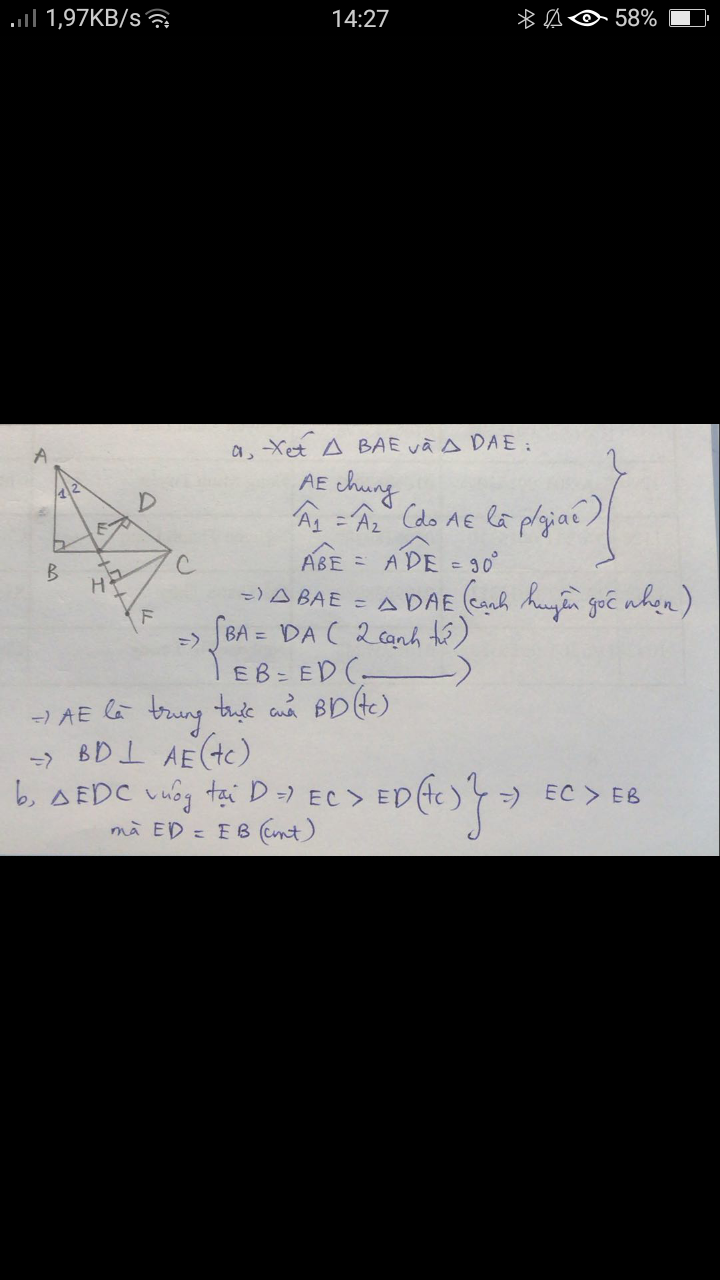Cho tam giác ADC VUÔNG TẠI D CÓ DF CE THUỘC AC , TRÊN TIA ĐỐI CỦA ED LẤY B SAO CHO EB:=ED
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc FEB+góc FBE=45+45=90 độ
=>EF vuông góc BC
b: ΔDFC vuông tại F có góc C=45 độ
nên ΔDFC vuông cân tại F
=>FD=FC
c: Xét ΔBEC có
EF,CA là đường cao
EF cắt CA tại D
=>D là trực tâm
=>BD vuông góc CE

a: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
b: Xét ΔABE và ΔADE có
AB=AD
\(\widehat{BAE}=\widehat{DAE}\)
AE chung
Do đó: ΔABE=ΔADE
Suy ra: EB=ED
c: Xét ΔBEG và ΔDEC có
BE=DE
\(\widehat{BEG}=\widehat{DEC}\)
EG=EC
Do đó: ΔBEG=ΔDEC
Suy ra: \(\widehat{EBG}=\widehat{EDC}\)
=>\(\widehat{EBG}+\widehat{ADE}=180^0\)
=>\(\widehat{EBG}+\widehat{EBA}=180^0\)
=>A,B,G thẳng hàng

a) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}=180^0-\widehat{A}-\widehat{C}\)
\(\Leftrightarrow\widehat{B}=180^0-60^0-40^0\)
hay \(\widehat{B}=80^0\)
Vậy: \(\widehat{B}=80^0\)
b) Xét ΔAEB và ΔCED có
AE=CE(E là trung điểm của AC)
\(\widehat{AEB}=\widehat{CED}\)(hai góc đối đỉnh)
EB=ED(gt)
Do đó: ΔAEB=ΔCED(c-g-c)
c) Xét ΔAED và ΔCEB có
AE=CE(E là trung điểm của AC)
\(\widehat{AED}=\widehat{CEB}\)(hai góc đối đỉnh)
ED=EB(gt)
Do đó: ΔAED=ΔCEB(c-g-c)
\(\Rightarrow\widehat{EAD}=\widehat{ECB}\)(hai góc tương ứng)
mà \(\widehat{EAD}\) và \(\widehat{ECB}\) là hai góc ở vị trí so le trong
nên AD//BC(Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: AD//BC(cmt)
\(EH\perp BC\)(gt)
Do đó: \(EH\perp AD\)(Định lí 2 từ vuông góc tới song song)