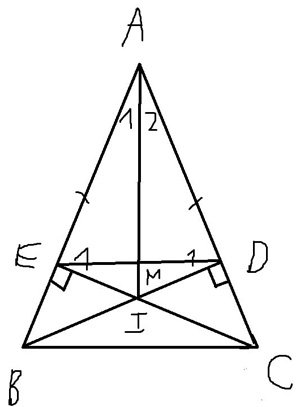
cho tam giác nhọn ABC có AB=AC . Kẻ BD ⊥ với AC tại D , kẻ CE⊥AB tại E . Gọi I là giao điểm của BD và CE.
a) CM △ ABD =△ACE
b) CM EI=DI
c) CM AI⊥BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 12 2020
bạn không được nói vậy , nói thế là khinh người khác và đây là nơi chúng ta giao lưu giúp nhau mà , nên bạn không được nói bậy như thế.
PL
18 tháng 12 2017
a) Cm BD = CE
\(\Delta ABC\)có AB = AC => \(\Delta ABC\)là tam giác cân tại A
Xét \(\Delta EBC\)và \(\Delta DCB\)có
Góc B = Góc C (Vì \(\Delta ABC\)cân)
BC : cạnh huyền chung
=> \(\Delta EBC=\Delta DCB\)(cạnh huyền - góc nhọn)
=> BD = CE (cạnh tương ứng) => ĐPCM
b) CM: EI = DI
Xét \(\Delta AHB\)và \(\Delta AHC\)có \(\hept{\begin{cases}AB=AC\left(gt\right)\\\widehat{B}=\widehat{C}\left(gt\right)\\BH=HC\left(gt\right)\end{cases}\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)}\)
=> \(\widehat{BAH}=\widehat{CAH}\)(góc tương ứng)
xét tam giác vuông AIE và tam giác vuông AID có
AI là cạnh huyền chung
\(\widehat{BAH}=\widehat{CAH}\) ( cmt)
do đó \(\Delta AIE=\Delta AID\) ( cạnh huyền - góc nhọn )
suy ra EI = ID ( 2 cạnh tương ứng )
c) \(\widehat{BAH}=\widehat{CAH}\) mà tia AH nằm giữa tia AB và AC nên AH là phân giác \(\widehat{BAC}\) (1)
\(\Delta AIE=\Delta AID\) suy ra \(\widehat{EAI}=\widehat{DAI}\) ( 2 góc tương ứng )
mà tia AI nằm giữa 2 tia AE và AD suy ra AI là phân giác \(\widehat{EAD}\) hay \(\widehat{BAD}\) (2)
từ (1) và (2) suy ra ba điểm A;I:H thẳng hàng
N
18 tháng 1 2021
Sửa lại đề : A < 90*
a, Chứng minh
\(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
\(\RightarrowĐPCM\)
b, CM được :
\(\widehat{ADE}\)\(=\)\(\widehat{ACB}\)\(=\)\(\frac{180'-\widehat{BAC}}{2}\)
\(\Rightarrow DE//BC\)
c, CM được : \(\widehat{IBC}=\widehat{ICB}\)
\(\RightarrowĐPCM\)
d, Gọi M là giao điểm của AI và BC ,
CM được AI là tia phân giác của góc \(\widehat{BAC}\), từ đó \(\widehat{AMB}\)\(=90'\)
\(\RightarrowĐPCM\)
18 tháng 12 2016
a) Xét tam giác ABD và tam giác ACE có
góc ADB = góc AEC = 90 độ
AB=AC
góc A: chung
=> tam giác ABD = tam giác ACE (cạnh huyền - góc nhọn)
=> BD=CE và AD=AE
b) Vì AB=AC và AE=AD => AB-AE=AC-AD => BE=CD
Xét tam giác OEB và tam giác ODC có
góc OEB = góc ODC = 90 độ
BE=CD
góc BOE = góc COD (đối đỉnh)
=> tam giác OEB = tam giác ODC => OB=OC
c) Xét tam giác AOB và tam giác AOC có
AB=AC
OB=OC
AO: cạnh chung
=> tam giác AOB = tam giác AOC (c.c.c)
=> góc OAB=góc OAC
=> AO la tia phân giác góc BAC
Bài mk lm như dzị ak
A
15 tháng 2 2018
a, tg ADB và tg AEC có^E1 = ^D1 = 90 độ
AB = AC
^A chung
=> tg ADB = tg AEC
=> AD = AE
=> tg ADE cân
b, tg ABI và tg ACI có
^E1 = ^D1 = 90 độ
AI chung
AB = AC
=> tg ABI = tg ACI
=> ^A1 = ^A2 ( góc t/ứ)
=> IB = IC ( cạnh t/ứ)
=> tg IBC cân
c, vì ^A1 = ^A2 ( câu b )
=> AI là tpg của góc EAD
19 tháng 12 2019
a, xét tam giác ABD và tam giác ACE có góc A chung
AB = AC (gt)
góc ADB = góc AEC = 90
=> tam giác ABD = tam giác ACE (ch-gn)
b, tam giác abd = tam giác ACE (câu a)
=> góc ABD = góc ACE (Đn)
AB = AC (gt) => tam giác ABC cân tại A (Đn) => góc ABC = góc ACB
có ABD + góc DBC = góc ABC
góc ACE + góc ECB = góc ACB
=> góc DBC = góc ECB
=> Tam giác IBC cân tại I
=> IB = IC
xét tam giác EIB và tam giác DIC có : góc EIB = góc DIC (đối đỉnh)
góc BEC = góc CDB = 90
=> tam giác EIB = tam giác DIC (ch-gn)
=> EI = ID (đn)
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: ΔABD=ΔACE
=>AD=AE
Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
=>EI=DI
c: ΔABD=ΔACE
=>BD=CE
BI+DI=BD
CI+EI=CE
mà EI=DI và BD=CE
nên BI=CI
IB=IC
AB=AC
Do đó: AI là đường trung trực của BC
=>AI\(\perp\)BC