Cho dãy số U 1 , U2 . . . Un
Dãy số trên có là dãy số cách đều không nếu Un = n2 + n
( Với mọi n lớn hơn hoặc bằng 1 )
Đố thánh nào làm được
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 3 2018
Chọn A
Trong bốn dãy số chỉ có yn=n/(n+1) < 1 nên có 1 dãy bị chặn trên
AH
Akai Haruma
Giáo viên
28 tháng 3 2021
Lời giải:
$\frac{u_{n-1}}{u_n}=\frac{n^2}{n^2-1}>0$ với mọi $n\geq 2$ nên $u_{n-1}, u_n$ luôn cùng dấu.
Mà $u_1=2017>0$ nên $u_n>0$ với mọi $n=1,2,...$
Mặt khác:
$n^2(u_{n-1}-u_n)=u_{n-1}>0\Rightarrow u_{n-1}>u_n$ nên dãy $(u_n)$ là dãy giảm.
Dãy giảm và bị chặn dưới nên $u_n$ hội tụ. Đặt $\lim u_n=a$.
Ta có: $a=n^2(a-a)\Rightarrow a=0$
Vậy $\lim u_n=0$
CM
22 tháng 7 2018
a) Khoảng cách từ un tới 0 trở nên rất nhỏ (gần bằng 0) khi n trở nên rất lớn
b) Bắt đầu từ số hạng u100 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,01
Bắt đầu từ số hạng u1000 của dãy số thì khoảng cách từ un đến 0 nhỏ hơn 0,001
CM
7 tháng 4 2018
Phương pháp:
Ứng với mỗi giá trị của n = 1, n = 2 ta tính các giá trị u2, u3 rồi tính giá trị của biểu thức.
Cách giải:
Ta có:
u n + 1 = u n + n , u 1 = 3
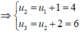
Chọn B
M
30 tháng 8 2023
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
Dãy số Un được gọi là dãy số cách đều khi : Un+1 - Un = d (Hằng số - Không phụ thuộc vào n) Nếu d.> 0 thì dãy số gọi là dãy số tăng, nếu d< 0 thì dãy số là dãy giảm.
Dãy số mà Un = n2 + n với \(\forall n\in N,n\ge1\).Ta xét hiệu Un+1 - Un = (n +1)2 + (n + 1) - (n2 + n) = 2n + 2 Không phải là hằng số (Vì hiệu này còn chứa n) Vậy dãy số đã cho không phải là dãy số cách đều.