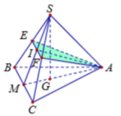
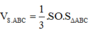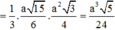cho hình chóp S.MNP có đáy MNP là tam giác đều. Gọi E,F,G lần lượt là trung điểm SM,SN,SP. Tìm ảnh của E,F,G trên mặt phẳng (MNP) qua phép chiếu theo phương SP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
16 tháng 11 2023
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 12 2020
a.
Trong mp (SAB) nối PM kéo dài cắt SB tại G
Trong mp (ABCD) nối PN cắt BC kéo dài tại H
\(\Rightarrow GH=\left(MNP\right)\cap\left(SBC\right)\)
b.
Nối SE cắt AD tại I, nối SF cắt BC tại K
Trong mp (ABCD), nối IK cắt PN kéo dài tại S
Trong mp (SBC), SF kéo dài cắt GH tại R
\(\Rightarrow RS\) là giao tuyến của (MNP) và (SEF)
Trong mp (SEF), nối RS và EF cắt nhau tại Q
\(\Rightarrow Q=EF\cap\left(MNP\right)\)
CM
3 tháng 3 2018
Chọn B
Ta có B C ⊥ S M . Gọi H là hình chiếu vuông góc của A trên SM. Do
và FE đi qua H.
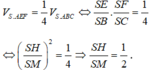
Vậy H là trung điểm cạnh SM. Suy ra tam giác SAM vuông cân tại A
⇒ S A = a 3 2 V S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8
CM
19 tháng 7 2019
Chọn B.
Gọi M là trung điểm BC, I = EF ∩ SM, suy ra I là trung điểm EF và SM.
Có 
=> AF = AE => AEF cân tại A => AI
⊥
EF.
Tam giác ASM có AI ⊥ SM và I là trung điểm SM nên ASM cân tại A, suy ra SA = AM = a 3 2 .
Gọi G là trọng tâm tam giác ABC 
Trong tam giác SAG có: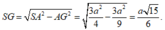 
Vậy thể tích khối chóp S.ABC là 
CM
8 tháng 3 2017
Đáp án A
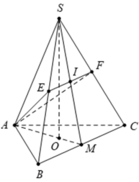
Gọi O là tâm của tam giác ABC, Vì I, M lần lượt là trung điểm của EF, BC
Theo bài ra, ta có 
cân tại A
Do đó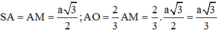 
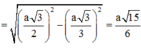
Vậy 
