Hai oto cùng khởi hành 1 lúc 2 tỉnh A và B cách nhau 400km đi ngược chiều và gặp nhau sau 5h. Nếu vận tốc mỗi xe không thay đổi nhưng xe đi chậm xuất phát trước xe kia 40 phút thì 2 xe gặp nhau sau 5h22' kể từ lúc xe chậm khởi hành. Tính vận tốc mỗi xe
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
16 tháng 1 2022
Gọi vận tốc ô tô khởi hành từ tỉnh A là x (km/h)
Gọi vận tốc ô tô khởi hành từ tỉnh B là y (km/h)
(ĐK: \(x>y>0\) )
Đổi: \(5h22'=\dfrac{161}{30}h,40'=\dfrac{2}{3}h\)
Hai ô tô đi ngược chiều và gặp nhau sau 5h nên ta có phương trình:
\(5x+5y=400\)
Quãng đường ô tô từ tỉnh A đi được đến lúc gặp nhau là: \(\dfrac{161}{30}x\left(km\right)\)
Quãng đường ô tô từ tỉnh B đi được đến lúc gặp nhau là: \(\dfrac{161}{30}y-\dfrac{2}{3}y=\dfrac{47}{10}y\left(km\right)\)
Do đó ta có phương trình:
\(\dfrac{161}{30}x+\dfrac{47}{10}y=400\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{161}{30}x+\dfrac{47}{10}y=400\\5x+5y=400\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=36\\y=44\end{matrix}\right.\)
Vậy vận tốc ô tô khởi hành từ tỉnh A là 36 (km/h)
Vận tốc ô tô khởi hành từ tỉnh B là 44 (km/h).
3 tháng 7 2023
5h22p-40p=4h42p=4,7h
5h22p=161/30h
Gọi vận tốc xe 1 và xe 2 lần lượt là a,b(a>b)
Theo đề, ta có: 5(a+b)=400 và 161/30b+4,7a=400
=>a=44 và b=36
11 tháng 3 2021
gọi vận tốc xe chậm và nhanh là x,y (km/h) với x,y>0
→độ dài AB:5x+5y=400
nếu xe chậm xuất phát trước 40p thì 2 xe gặp nhau sau 5h22p
→thời gian xe chậm đi là :5h22p=161/30h
Thời gian xe nhanh đi:5h22p -40p =4h42p =47/10h
→Độ dài AB :161/30x +47/10y=400
theo bài ra ta có hệ: 5x+5y=400 và 161/30x +47/10y=400
→ x+y=80 và 161x+141y=12000
→x=36 ,y=44 (km/h)
CM
6 tháng 7 2018
Đáp án A
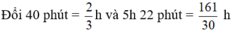
Gọi vận tốc của xe nhanh là x km/h
Gọi vận tốc của xe chậm là y km/h (điều kiện: x> y > 0)
Hai xe cùng khởi hành một lúc và đi ngược chiều sau 5h gặp nhau nên ta có phương trình
Vậy vận tốc của xe nhanh là 44 km/h
Vận tốc của xe chậm là 36 km/h.
11 tháng 3 2021
gọi vận tốc xe chậm và nhanh là x,y (km/h) với x,y>0
→độ dài AB:5x+5y=400
nếu xe chậm xuất phát trước 40p thì 2 xe gặp nhau sau 5h22p
→thời gian xe chậm đi là :5h22p=161/30h
Thời gian xe nhanh đi:5h22p -40p =4h42p =47/10h
→Độ dài AB :161/30x +47/10y=400
theo bài ra ta có hệ: 5x+5y=400 và 161/30x +47/10y=400
→ x+y=80 và 161x+141y=12000
→x=36 ,y=44 (km/h)
=>A
11 tháng 3 2021
Gọi thời gian dự định đi từ A đến B là x ( giờ) ( x>0)
=> quãng đường AB : 12x
1h20'=1/3=4/3h
Theo bài ra, ta có pt:
\(\frac{1}{3}.\frac{12x}{2}+\frac{20}{60}+\frac{2}{3}.\frac{12x}{36}=x-\frac{4}{3}\)
giải ra được \(x=\frac{15}{4}\) (giờ)
Vậy độ dài quãng đường AB : 12.\(\frac{15}{4}=45\left(km\right)\)
11 tháng 3 2021
gọi vận tốc xe chậm và nhanh là x,y (km/h) với x,y>0
→độ dài AB:5x+5y=400
nếu xe chậm xuất phát trước 40p thì 2 xe gặp nhau sau 5h22p
→thời gian xe chậm đi là :5h22p=161/30h
Thời gian xe nhanh đi:5h22p -40p =4h42p =47/10h
→Độ dài AB :161/30x +47/10y=400
Theo bài ra ta có hệ: 5x+5y=400 và 161/30x +47/10y=400
→ x+y=80 và 161x+141y=12000
Vậy : x=36 ,y=44 (km/h)
AH
Akai Haruma
Giáo viên
20 tháng 12 2023
Lời giải:
Đổi 40' = $\frac{2}{3}$ giờ
Gọi vận tốc xe nhanh là a và xe chậm là b (đơn vị: km/h)
Theo bài ra ta có:
$a+b=400:5=80(1)$
Kể từ khi xe nhanh xuất phát, hai xe đi ngược chiều nhau 1 quãng đường có độ dài $400-\frac{2}{3}b$ (km). Hai xe gặp nhau sau $5h22'=\frac{161}{30}$ giờ. Khi đó ta có:
$a+b=(400-\frac{2}{3}b):\frac{161}{30}(2)$
Từ $(1); (2)\Rightarrow (400-\frac{2}{3}b): \frac{161}{30}=80$
$\Rightarrow b=-44$ (km) (vô lý)
TN
18 tháng 2 2022
Bg: Gọi vận tốc ôtô khởi hành từ tỉnh A Ɩà x (km/h)
Gọi vận tốc ôtô khởi hành từ tỉnh B Ɩà Ɩà y (km/h)
(ĐK: x > y > 0)．Đổi 5h22′ = 161/30h， 40′ = 2/3h
Hai ôtô đi ngược chiều nhau ѵà gặp nhau sau 5h nên ta có phương trình 5x + 5y = 400
Quãng đường mà ôtô từ đỉnh A đi được đến lúc gặp nhau Ɩà:
161/30x (km)
Quãng đường mà ôtô từ đỉnh B đi được đến lúc gặp nhau Ɩà:
161/30y – 2/3y = 47/10y (km)
Do đó ta có phương trình:
161/30x + 47/10y = 400
=> Hệ phương trình: {161/30x + 47/10y = 400; 5x + 5y = 400}
⇔ {5x + 5y = 400; 161x + 141y = 12000}
⇔ {161x + 161y = 12880; 161x + 141y = 12000}
⇔ {y = 44; 161x + 141y = 12000} ⇔ {x = 36; y = 44} (thỏa mãn)
⇒ Vận tốc c̠ủa̠ ôtô khởi hành từ A Ɩà 36 (km/h).
Vận tốc c̠ủa̠ ôtô khởi hành từ B Ɩà 44 (km/h).
DM
18 tháng 5 2017
Gọi x (km/h) là vận tốc của xe chạy nhanh, y (km/h) là vận tốc xe chạy chậm.
Theo đề : Hai xe khởi hành cùng lúc, đi ngược chiều và gặp nhau sau 5h, ta có :
\(5\left(x+y\right)=400\Leftrightarrow x+y=80\)(1)
Theo đề vế sau, xe đi chậm đến lúc gặp nhau sau 5h22' \(=\dfrac{161}{30}\left(h\right)\)
=> Xe nhanh đi hết \(\dfrac{161}{30}-\dfrac{2}{3}=\dfrac{141}{30}\left(h\right)\)
\(\Leftrightarrow\dfrac{141}{30}x+\dfrac{161}{30}y=400\left(2\right)\)
(1) , (2) Ta có hpt :
\(\left\{{}\begin{matrix}x+y=80\\\dfrac{141}{30}x+\dfrac{161}{30}y=400\end{matrix}\right.\)
Giải hệ => \(\left\{{}\begin{matrix}x=44\\y=36\end{matrix}\right.\).
Vậy xe nhanh đi vs vận tốc 44 km/h, xe chậm 36 km/h.
18 tháng 5 2017
Gọi vận tốc xe chậm và xe nhanh lần lượt là x km/h và y km/h(x,y>0)
=>Độ dài quãng đường AB:5x+5y=400(km)
Nếu xe chậm xuất phát trước 40p thì 2 xe gặp nhau sau 5h22p
=>Thời gian xe chậm đi là 5h22p=\(\dfrac{161}{30}h\)
Thời gian xe nhanh đi là:5h22p-40p=4h42p=\(\dfrac{47}{10}h\)
=>Độ dài quãng đường AB là:\(\dfrac{161}{30}x+\dfrac{47}{10}y=400\)(km)
Theo bài ra ta có hệ PT:
\(\left\{{}\begin{matrix}5x+5y=400\\\dfrac{161}{30}x+\dfrac{47}{10}y=400\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x+y=80\\161x+141y=12000\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}x=36\\y=44\end{matrix}\right.\)
Vậy...
TH
2 tháng 2 2021
Gọi vận tốc xe máy và ô tô lần lượt là: x; y (km/h)
Nếu chạy ngược chiều, hai xe gặp nhau lúc 5h; tức là tổng quãng đường hai xe đi trong 5h đó bằng độ dài AB: 5x + 5y = 350 => x + y = 70 (1)
Nếu chạy cùng chiều, khi hai xe gặp nhau tức là chúng đã đi quãng đường bằng nhau:
( với xe máy khời hành trước ô tô 1h và chúng gặp nhau sau 3h kể từ lúc ô tô xuất phát)
4x = 3y (2)
giải hệ phương trình (1) và (2) ta được: x = 30; y = 40 (km/h)
Vậy, vận tốc xe máy và ô tô lần lượt là 30 km/h và 40 km/h.
\(40p=\dfrac{2}{3}h;5h22'=\dfrac{161}{30}h\)
Gọi vận tốc xe thứ nhất là x(km/h), vận tốc xe thứ hai là y(km/h)
(Điều kiện: x>0 và y>0)
Hai xe nếu khởi hành cùng lúc thì sẽ gặp nhau sau 5h nên độ dài quãng đường hai xe đi được sẽ là:
5x+5y=400
=>5(x+y)=400
=>\(x+y=\dfrac{400}{5}=80\)
Thời gian xe thứ hai đi từ lúc khởi hành đến chỗ gặp nhau là \(5h22'=\dfrac{161}{30}\left(h\right)\)
Thời gian xe thứ nhất đi từ lúc khởi hành đến chỗ gặp nhau là \(\dfrac{161}{30}-\dfrac{2}{3}=\dfrac{161-20}{30}=\dfrac{141}{30}\left(h\right)\)
Độ dài quãng đường xe thứ nhất đi từ lúc khởi hành đến chỗ gặp là: \(\dfrac{141}{30}x\left(km\right)\)
Độ dài quãng đường xe thứ hai đi từ lúc khởi hành đến chỗ gặp là \(\dfrac{161}{30}y\left(km\right)\)
Tổng độ dài quãng đường hai xe đi được là 400km nên ta có: \(\dfrac{141}{30}x+\dfrac{161}{30}y=400\)
Do đó, ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=80\\\dfrac{141}{30}x+\dfrac{161}{30}y=400\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=80\\141x+161y=400\cdot30=12000\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}141x+141y=11280\\141x+161y=12000\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-20y=-720\\x+y=80\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=36\\x=44\end{matrix}\right.\left(nhận\right)\)
Vậy: vận tốc xe thứ nhất là 44km/h
vận tốc xe thứ hai là 36km/h