Tìm x thuộc z biết 4x-5 chia hết cho 2x-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
0
23 tháng 2 2017
a,\(\dfrac{3x+5}{x-2}=3+\dfrac{11}{x-2}\)
\((3x+5)\vdots (x-2)\) \(\Rightarrow\)\(\dfrac{3x+5}{x-2}\)nguyên \(\Rightarrow \dfrac{11}{x-2}\)nguyên
\(\Rightarrow 11\vdots(x-2)\Rightarrow (x-2)\in Ư(11)=\{\pm1;\pm11\}\)
\(\Rightarrow x\in\{-9;1;3;13\}\)
b,\(\dfrac{2-4x}{x-1}=-4-\dfrac{2}{x-1}\)
\((2-4x)\vdots(x-1)\Rightarrow \dfrac{2-4x}{x-1}\)nguyên\(\Rightarrow \dfrac{2}{x-1}\)nguyên
\(\Rightarrow 2\vdots(x-1)\Rightarrow (x-1)\inƯ(2)=\{\pm1;\pm2\}\\\Rightarrow x\in\{-1;0;2;3\}\)
c,\(\dfrac{x^{2}-x+2}{x-1}=\dfrac{x(x-1)+2}{x-1}=x+\dfrac{2}{x-1}\)
\((x^{2}-x+2)\vdots(x-1)\)\(\Rightarrow \dfrac{x^{2}-x+2}{x-1}\)nguyên \(x+\dfrac{2}{x-1}\)nguyên\(\Rightarrow \dfrac{2}{x-1}\)nguyên
\(\Rightarrow 2\vdots(x-1)\Rightarrow (x-1)\inƯ(2)=\{\pm1;\pm2\}\\\Rightarrow x\in\{-1;0;2;3\}\)
d,\(\dfrac{x^{2}+2x+4}{x+1}=\dfrac{(x+1)^{2}+3}{x+1}=x+1+\dfrac{3}{x+1}\)
\((x^{2}+2x+4)\vdots(x+1)\Rightarrow \dfrac{x^{2}+2x+4}{x+1}\in Z\Rightarrow \dfrac{3}{x+1}\in Z\\\Rightarrow3\vdots(x+1)\Rightarrow (x+1)\in Ư(3)=\{\pm1;\pm3\}\\\Rightarrow x\in\{-4;-2;0;2\}\)
NN
4
2 tháng 12 2023
4x + 7 chia hết cho 2x + 1
= > 2( 2x + 1 ) +5 chia hết cho 2x + 1
= > 5 chia hết cho 2x + 1 ( với x \(\in Z\) )
= > 2x + 1 thuộc Ư ( 5 ) \(\in\left\{\pm1;\pm5\right\}\)
Với : 2x + 1 = -1 <=> x = -1 ( t/m )
2x + 1 = 1 <=> x = 0 ( t/m )
2x + 1 = 5 <=> x = 2 ( t/m )
2x + 1 = -5 <=> x = -3 ( t/m )
Vậy để 4x + 7 chia hết cho 2x +1 thì các giá trị nguyên \(x\in\left\{-3;-1;0;2\right\}\)
2 tháng 12 2023
4x + 7 chia hết cho 2x + 1
Mà 4x + 2 chia hết cho 2x + 1
=> 4x + 7 - 4x + 2 chia hết cho 2x + 1
5 chia hết cho 2x + 1
=> 2x + 1 € Ư(5)
=> x € { 0; 2}
18 tháng 1 2017
4x + 5 chia hết cho 2x + 1
4x + 2 + 3 chia hết cho 2x + 1
2(2x + 1) + 3 chia hết cho 2x + 1
=> 3 chia hết cho 2x + 1
=> 2x + 1 thuộc Ư(3) = {1 ; -1 ; 3 ; -3}
Ta ó bảng sau :
| 2x + 1 | 1 | -1 | 3 | -3 |
| x | 0 | -1 | 1 | -2 |
18 tháng 1 2017
Ta có : 4x+5=2(2x+1)+3
Để 4x+5 chia hết 2x+1
Nên 3 chia hết 2x+1
Suy ra 2x+1 thuộc Ư(3) = {1;3;-1;-3}
Nếu 2x+1 = 1 thì x = 0
Nếu 2x+1 = 3 thì x = 1
Nếu 2x+1 = -1 thì x = -1
Nếu 2x+1 = -3 thì x = -2
Vậy x thuộc {-2;-1;0;1}
BN
0
TN
30 tháng 1 2016
a)<=>(x+1)+2 chia hết x+1
=>2 chia hết x+1
=>x+1\(\in\){1,-1,2,-2}
=>x\(\in\){0,-2,1,-3}
b)<=>3(x-2)+7 chia hết x-2
=>7 chia hết x-2
=>x-2\(\in\){1,-1,7,-7}
=>x\(\in\){3,1,9,-5}
c,d,e tương tự
6 tháng 3 2020
\(a,2x+1⋮x-2\)
\(=>2.\left(x-2\right)+5⋮x-2\)
Do \(2.\left(x-2\right)⋮x-2\)
\(=>5⋮x-2\)
\(=>x-2\inƯ\left(5\right)\)
Nên ta có bảng sau :
| x-2 | 1 | 5 | -1 | -5 |
| x | 3 | 7 | 1 | -3 |
Vậy ...
\(b,3x+5⋮x\)
Do \(3x⋮x=>5⋮x\)
\(=>x\inƯ\left(5\right)\)
Nên ta có bảng sau :
| x | 1 | 5 | -1 | -5 |
Vậy ...
\(c,4x+1⋮2x+3\)
\(=>2.\left(2x+3\right)-5⋮2x+3\)
Do \(2.\left(2x+3\right)⋮2x+3\)
\(=>5⋮2x+3\)
\(=>2x+3\inƯ\left(5\right)\)
Nên ta có bảng sau :
| 2x+3 | 1 | 5 | -1 | -5 |
| 2x | -2 | 2 | -4 | -8 |
| x | -1 | 1 | -2 | -4 |
Vậy ...
6 tháng 3 2020
a) Ta có: 2x+1=2(x-2)+5
Để 2x+1 chia hết cho x-2 thì 2(x-2)+5 chia hết cho x-2
Vì 2(x-2) chia hết cho x-2
=> 5 chia hết cho x-2
Vì x thuộc Z => z-2 thuộc Ư (5)={-5;-1;1;5}
Nếu x-2=-5 => x=-3
Nếu x-2=-1 => x=1
Nếu x-2=1 => x=3
Nếu x-1=5 => x=6
b) Ta có 3x chia hết cho x với mọi x
=> Để 3x+5 chia hết cho x thì 5 chia hết cho x
Vì x thuộc Z => x thuộc Ư (5)={-5;-1;1;5}
c) Ta có: 4x+11=2(2x+3)+5
Để 4x+11 chia hết cho 2x+3 thì 2(2x+3)+5 chia hết cho 2x+3
Vì 2(2x+3) chia hết cho 2x+3 => 5 chia hết cho 2x+3
Vì x thuộc Z => 2x+3 thuộc Ư (5)={-5;-1;1;5}
Nếu 2x+3=-5 => 2x=-8 => x=-4
Nếu 2x+3=-1 => 2x=-4 => x=-2
Nếu 2x+3=1 => 2x=-2 => x=-1
Nếu 2x+3=5 => 2x=2 => x=1
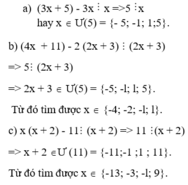
Do 2x-1 chia hết cho 2x-1
=> 2(2x-1) chai hết cho 2x-1
=> 4x-2 chia hết cho 2x-1 (1)
Mà 4x-5 chia hết cho 2x-1 (2)
Từ (1) và (2) => (4x-2) - (4x-5) chia hết cho 2x-1
=> 4x - 2 - 4x +5 chia hết cho 2x-1
=> 3 chia hết cho 2x-1
=> 2x-1 thuộc Ư(3) là -3;-1;1;3.
=> 2x thuộc tập hợp -2;0;2;4
=> x thuộc tập hợp -1;0;1;2 ; với x thuộc Z
Vậy x thuộc tập hợp -1;0;1;2 với X thuộc Z.