Cho tam giác ABC có A = 68 độ. Các phân giác ngoài của góc B và C cắt nhau tại K. Tính BKC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

30 tháng 7 2015
Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ

SU
31 tháng 7 2015
ai bit thi tra loi giup mik di mot chut nua la mik phai nop bai r
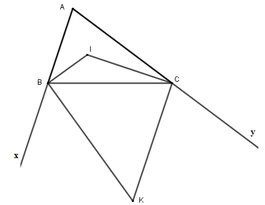

A B C K x y
Xét tg ABC có
\(\widehat{B}+\widehat{C}=180^o-\widehat{A}=180^o-68^o=112^o\)
\(\widehat{KBC}=\dfrac{\widehat{ABx}-\widehat{B}}{2}=\dfrac{180^o-\widehat{B}}{2}=90^o-\dfrac{\widehat{B}}{2}\)
\(\widehat{KCB}=\dfrac{\widehat{ACy}-\widehat{C}}{2}=\dfrac{180^o-\widehat{C}}{2}=90^o-\dfrac{\widehat{C}}{2}\)
Xét tg KBC có
\(\widehat{BKC}=180^o-\left(\widehat{KBC}+\widehat{KCB}\right)=\)
\(=180^o-\left(90^o-\dfrac{\widehat{B}}{2}+90^o-\dfrac{\widehat{C}}{2}\right)=\dfrac{\widehat{B}+\widehat{C}}{2}=\dfrac{112^o}{2}=56^o\)