Cho định lý : nếu 1 đường thẳng cách 2 đuờng thẳng và trong các góc tạo thành có 1 cặp góc sole trong bằng nhau thì 2 góc trong cùng phía bù nhau Vẽ hình, giả thiết, kết luận, chứng minh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
15 tháng 10 2023
Giả thiết: "Đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau" ; Kết luận: " Hai góc so le trong còn lại bằng nhau."
4 tháng 2 2022
Bài 1:
| GT | \(\widehat{A}+\widehat{B}=90^0;\widehat{C}+\widehat{B}=90^0\) |
| KL | \(\widehat{A}=\widehat{C}\) |
Ta có: \(\widehat{A}+\widehat{B}=90^0\)
nên \(\widehat{A}=90^0-\widehat{B}\left(1\right)\)
Ta có: \(\widehat{C}+\widehat{B}=90^0\)
nên \(\widehat{C}=90^0-\widehat{B}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{C}\)
H
28 tháng 9 2018
Chứng minh định lí
A1 + B1 = 1800
Mà A1 + A2 = 1800 ( 2 góc kề bù )
\(\Rightarrow\)B1 = A2
Mà B1 và A2 là 2 góc đồng vị
\(\Rightarrow\)a // b
HV
28 tháng 9 2018
GT:Nếu hai đg thẳng a,b cất đg thảng c.............bù nhau
KL:Thì a và b song song với nhau
8 tháng 8 2016
GT:ĐT a,b cắt c tạo thành một cập góc bù nhau
KL:a,b //
chứng minh
ta gọi hai điểm cắt nhau giữa ĐT a,b và c là A,B
Ta có tổng cặp góc trong cùng phía bàng 180 độ
Ta thấy :mỗi cặp góc trong cùng phía đều đối đỉnh với một góc ngoài cùng phía
=>a//b
8 tháng 8 2016
Chứng minh định lí: Theo đề bài góc A1 + B1 = 180o
Ta có: góc A1 + A2 = 180o (tính chất kề bù)
Góc B1 = A2 mà hai góc này đồng vị => a//b
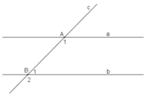
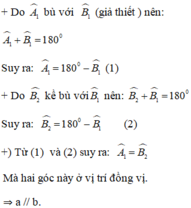
a cắt c tại A, a cắt b tại D
\(\widehat{A_1}=\widehat{D_3}\)
\(\widehat{A_1}=\widehat{D_3}\)(hai góc so le trong bằng nhau)
mà \(\widehat{A_1}+\widehat{A_2}=180^0\)
nên \(\widehat{A_2}+\widehat{D_3}=180^0\)(ĐPCM)