a) Tìm số tự nhiên n sao cho 2n + 5 chia hết cho n + 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 11 2018
1)2n+5-2n-1
=>4 chia hết cho 2n-1
ước của 4 là 1 2 4
2n-1=1=>n=.....
tiếp với 2 và 4 nhé
NT
3
HB
24 tháng 9 2017
n+9 chia hết cho n-2
n+9= (n-2)+11
Để n+9 chia hết cho n-2 thì 11 chia hết cho n-2
n-2 thuộc Ư(11)={1,11}
n-2=1 => n=1+2 => n=3
n-2=11=> n=11+2=> n=13
b) 2n+5 chia hết cho n+2
2n+5=2(n+2)+1
để 2n+5 chia hết cho n+2 thì 1: n+2
=> n+2 thuộc Ư(1)={1}
n+2=1 => n=1-2 => n=-1
c) 6n-16 chia hết cho 2n+1
6n-16=3(2n+1)-19
để 6n-16 chia hết cho 2n+1 thì 19 chia hết cho 2n+1
=> 2n+1 thuộc Ư(19)={19}
=> 2n+1=1 => 2n=1+1 => 2n=2 => n=2:2 => n=1
tương tự như vậy bn tự giải số còn lại nha
TM
24 tháng 9 2017
a)\(n+9=n-2+11\)chia hết cho n-2
mà n-2 chia hết cho n-2 => 11 chia hết cho n-2
=>\(n-2\inƯ\left(11\right)=\left\{-11;-1;1;11\right\}\)
\(\Rightarrow n\in\left\{-9;1;3;13\right\}\)
b)\(2n+5=\left(2n+4\right)+1=2\left(n+2\right)+1\) chia hết cho n+2
mà 2(n+2) chia hết cho n+2 => 1 chia hết cho n+2
=>\(n+2\in\left\{-1;1\right\}\)
=>\(n\in\left\{-3;-1\right\}\)
17 tháng 8 2016
a) n + 2 chia hết cho n - 1
=> n - 1 + 3 chia hết cho n - 1
Do n - 1 chia hết cho n - 1 => 3 chia hết cho n - 1
Mà n thuộc N => n - 1 > hoặc = -1
=> n - 1 thuộc {-1 ; 1 ; 3}
=> n thuộc {0 ; 2 ; 4}
Những câu còn lại lm tương tự
17 tháng 8 2016
Giải:
a) \(n+2⋮n-1\)
\(\Rightarrow\left(n-1\right)+3⋮n-1\)
\(\Rightarrow3⋮n-1\)
\(\Rightarrow n-1\in\left\{\pm1;\pm3\right\}\)
+) \(n-1=1\Rightarrow n=2\)
+) \(n-1=-1\Rightarrow n=0\)
+) \(n-1=3\Rightarrow n=4\)
+) \(n-1=-3\Rightarrow n=-2\)
Vậy \(n\in\left\{2;0;4;-2\right\}\)
b) \(2n+7⋮n+1\)
\(\Rightarrow\left(2n+2\right)+5⋮n+1\)
\(\Rightarrow2\left(n+1\right)+5⋮n+1\)
\(\Rightarrow5⋮n+1\)
\(\Rightarrow n+1\in\left\{\pm1;\pm5\right\}\)
+) \(n+1=1\Rightarrow n=0\)
+) \(n+1=-1\Rightarrow n=-2\)
+) \(n+1=3\Rightarrow n=2\)
+) \(n+1=-3\Rightarrow n=-4\)
Vậy \(n\in\left\{0;-2;2;-4\right\}\)
5 tháng 7 2018
Vì 3 n chia hết cho (5-2n)
=>2.3n+3(5-2n)=15 chia hết cho 5-2n
=>5-2n thuộc Ư(15)={1,3,5,15,-1,-3-5-15}
Mặt khác 5-2n nhỏ hơn hoặc bằng 5
5-2n thuộc {-15,-5,-3,-1,1,3,5}
=>N thuộc { 10,5,4,3,2,1,0}
Vì 3n chia hết cho 5-2n
=>2.3n+3(5-2n)=15 chia hết cho 5 - 2n
=> 5-2n thuộc U (15)€{1,3,5,15,-1,-3,-5,-15}
Mặt khác 5 trừ 2 n nhỏ hơn hoặc bằng 5
=>5-2n€{-15,-5,-3,-1,1,3,5}
=>N€{10,5,4,3,2,1,0}
DM
1
2 tháng 11 2021
\(a,\Rightarrow n+1+4⋮n+1\\ \Rightarrow n+1\inƯ\left(4\right)=\left\{4\right\}\left(n+1>1+1=2\right)\\ \Rightarrow n=3\\ b,\Rightarrow2\left(n-1\right)+3⋮n-1\\ \Rightarrow n-1\inƯ\left(3\right)=\left\{1;3\right\}\\ \Rightarrow n\in\left\{2;4\right\}\)
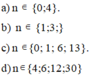
Ta có:
2n + 5 = 2n + 4 + 1
= 2(n + 2) + 1
Để (2n + 5) ⋮ (n + 2) thì 1 ⋮ (n + 2)
⇒ n + 2 ∈ Ư(1) = {-1; 1}
⇒ n ∈ {-3; -1}
Mà n ∈ ℕ
⇒ Không tìm được n ∈ ℕ thỏa mãn đề bài
2n+5 chia hết cho n+2
=>\(2n+4+1⋮n+2\)
=>\(1⋮n+2\)
=>\(n+2\in\left\{1;-1\right\}\)
=>\(n\in\left\{-1;-3\right\}\)
mà n>=0
nên \(n\in\varnothing\)