
Giúp tớ câu 6 với ạaa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 8:
\(x^2+\left(2m+1\right)x-m^2=0\)
a=1; b=2m+1; c=-m2
Vì ac<=0 nên phương trình luôn có nghiệm
Theo đề, ta có: \(A=\left(x_1+x_2\right)^2-8x_1x_2\)
\(=\left(2m+1\right)^2-8\left(-m^2\right)\)
\(=4m^2+4m+1+8m^2=12m^2+4m+1\)
\(=12\left(m^2+\dfrac{1}{3}m+\dfrac{1}{12}\right)\)
\(=12\left(m^2+2\cdot m\cdot\dfrac{1}{6}+\dfrac{1}{36}+\dfrac{1}{18}\right)\)
\(=12\left(m+\dfrac{1}{6}\right)^2+\dfrac{2}{3}\ge\dfrac{2}{3}\forall m\)
Dấu '=' xảy ra khi m=-1/6

\(=\dfrac{\sqrt{x}+2-\sqrt{x}}{x-4}\cdot\dfrac{x+2}{1}=\dfrac{2\left(x+2\right)}{x-4}=\dfrac{2x+4}{x-4}\)

Câu 2:
uses crt;
var a:array[1..100]of integer;
i,n,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
t:=0;
for i:=1 to n do
if (4<a[i]) and (a[i]<15) then t:=t+a[i];
writeln(t);
readln;
end.

Bài 4:
a: \(C=\frac13\left(-6x^2y^2\right)^2\cdot\left(\frac12x^3y\right)=\frac13\cdot36x^4y^4\cdot\frac12x^3y\)
\(=36\cdot\frac13\cdot\frac12\cdot x^4\cdot x^3\cdot y^4\cdot y=6x^7y^5\)
b: Khi x=1;y=-1 thì \(C=6\cdot1^7\cdot\left(-1\right)^5=6\cdot1\cdot\left(-1\right)=-6\)
Bài 3:
\(D=\left(-\frac37x^2y\right)\left(\frac79x^2y^2\right)=-\frac37\cdot\frac79\cdot x^2\cdot x^2\cdot y\cdot y^2=-\frac13x^4y^3\)
hệ số là -1/3
Bậc là 4+3=7
Biến là \(x^4;y^3\)

1 ........will be rebuilt next year
2 .......met each other for ten years
3 ..... of Liberty was presented to the United State by France in 1876
4 ........ too high for the children to reach
5 ...... on animals should be stopped
6 ..... her child not to cry
7 .......mind if I turn on the television?
8 ......... rather you didn't use the office phone
9.........asked the students not to throw things away
10 ........ suggest that we go to the movie now
11 ....goes to Ho Chi Minh City in order to visit his friend
12 smoked
13 ..... interesting to learn ENglish
14She shows me where to get the tickets
15 The boy who is talking to Lan is my classmate
16 The wall has been painted white
17 .......told to go away
18 ...... will be looked after carefully
19 She asked me if I was good at Maths
20 They said that they had attended course of cooking
---------------------------------------------------------------------------------
1 without
2 for
-Tham khảo c2 bV
3 at - on
4 of - from
-Tham khảo c4 bV
5 to - on
6 of
7 among
8 of
9 into
10 for

a) \(A=\left(x+5\right)^2-\left(x+3\right)^2\)
\(=\left[\left(x+5\right)-\left(x+3\right)\right]\left[\left(x+5\right)+\left(x+3\right)\right]\)
\(=\left(x+5-x-3\right)\left(x+5+x+3\right)\)
\(=2\left(2x+8\right)\)
\(=4x+16\)
b) \(B=\left(4x+1\right)^2-\left(2x+1\right)^2\)
\(=\left[\left(4x+1\right)-\left(2x+1\right)\right]\left[\left(4x+1\right)+\left(2x+1\right)\right]\)
\(=\left(4x+1-2x-1\right)\left(4x+1+2x+1\right)\)
\(=2x\left(6x+2\right)\)
\(=12x^2+4x\)
c) \(C=\left(3-4x\right)^2-\left(2x-1\right)\left(8x-9\right)\)
\(=9-24x+16x^2-16x^2+18x+8x-9\)
\(=\left(16x^2-16x^2\right)+\left(-24x+18x+8x\right)+\left(9-9\right)\)
\(=2x\)
d) \(D=\left(4+2x^2\right)-\left(1-4x\right)\left(4-x\right)\)
\(=4+2x^2-4+x+16x-4x^2\)
\(=\left(2x^2-4x^2\right)+\left(x+16x\right)+\left(4-4\right)\)
\(=-2x^2+17x\)
e) \(E=\left(2-3x\right)^2-2\left(2-3x\right)\left(3x+5\right)+\left(3x+5\right)^2\)
\(=\left(2-3x+3x+5\right)^2\)
\(=7^2\)
\(=49\)

Tôi đi học được bố cục theo dòng hồi tưởng của nhân vật "tôi” về những kỉ niệm buổi tựu trường. Tiết trời vào những ngày cuối thu, hình ảnh các em nhỏ đến trường gợi cho nhân vật “tôi” nhớ lại ngày đầu tiên đi học. "Tôi" nhớ lại con đường cùng mẹ đến trường, cảnh vật trên đường vốn rất quen nhưng lần này tự nhiên thấy lạ, “tôi” cảm thấy có sự thay đổi lớn trong lòng mình. Đó là cảm giác trang trọng và đứng đắn trong chiếc áo vải dù đen dài, cùng mấy quyển vở mới trên tay. Bàn tay cẩn thận, nâng niu mấy quyển vở, lúng túng muốn thử sức nên xin mẹ được cầm cả bút, thước như các bạn khác. Khi nhìn thấy ngôi trường ngày khai giảng, "tôi" thấy ngạc nhiên vì sân trường hôm nay dày đặc cả người, ai cũng ăn mặc sạch sẽ, gương mặt tươi vui và sáng sủa. Ngôi trường vừa xinh xắn vừa oai nghiêm khác thường, “tôi” cảm thấy mình bé nhỏ, do đó lo sợ vẩn vơ. Đặc biệt, lúc ngồi vào chỗ của mình trong giờ học đầu tiên, nghe thầy giáo gọi tên, bắt đầu học bài học thứ nhất,... nhân vật chính của thiên truyện vừa thấy hồi hộp, ngỡ ngàng lại vừa tự tin, sung sướng.


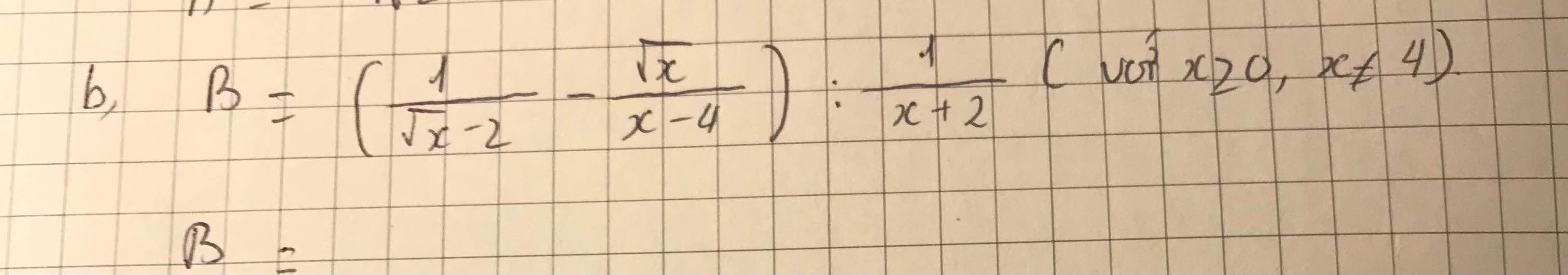



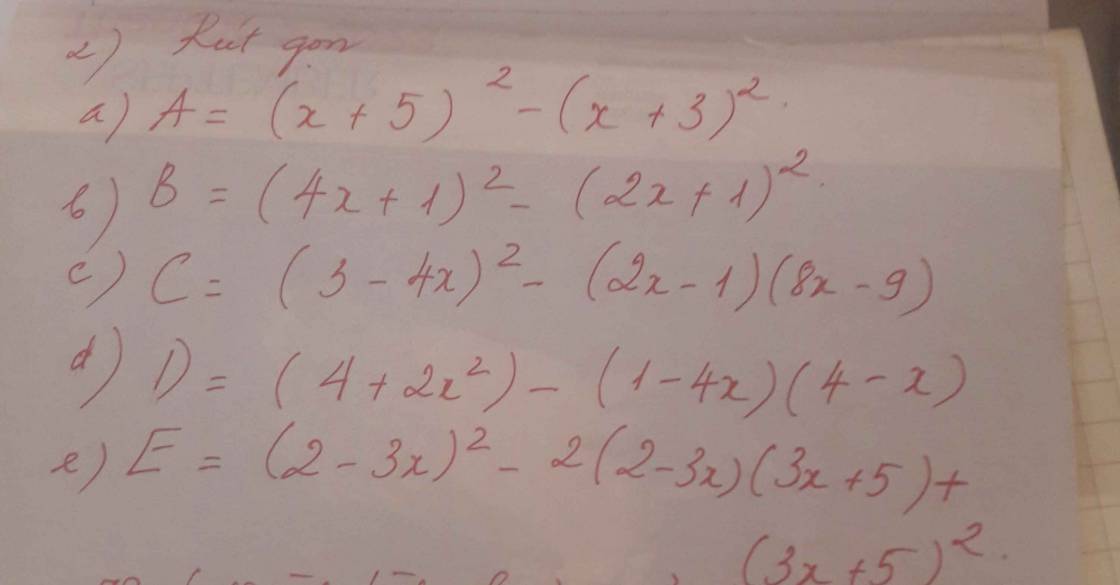
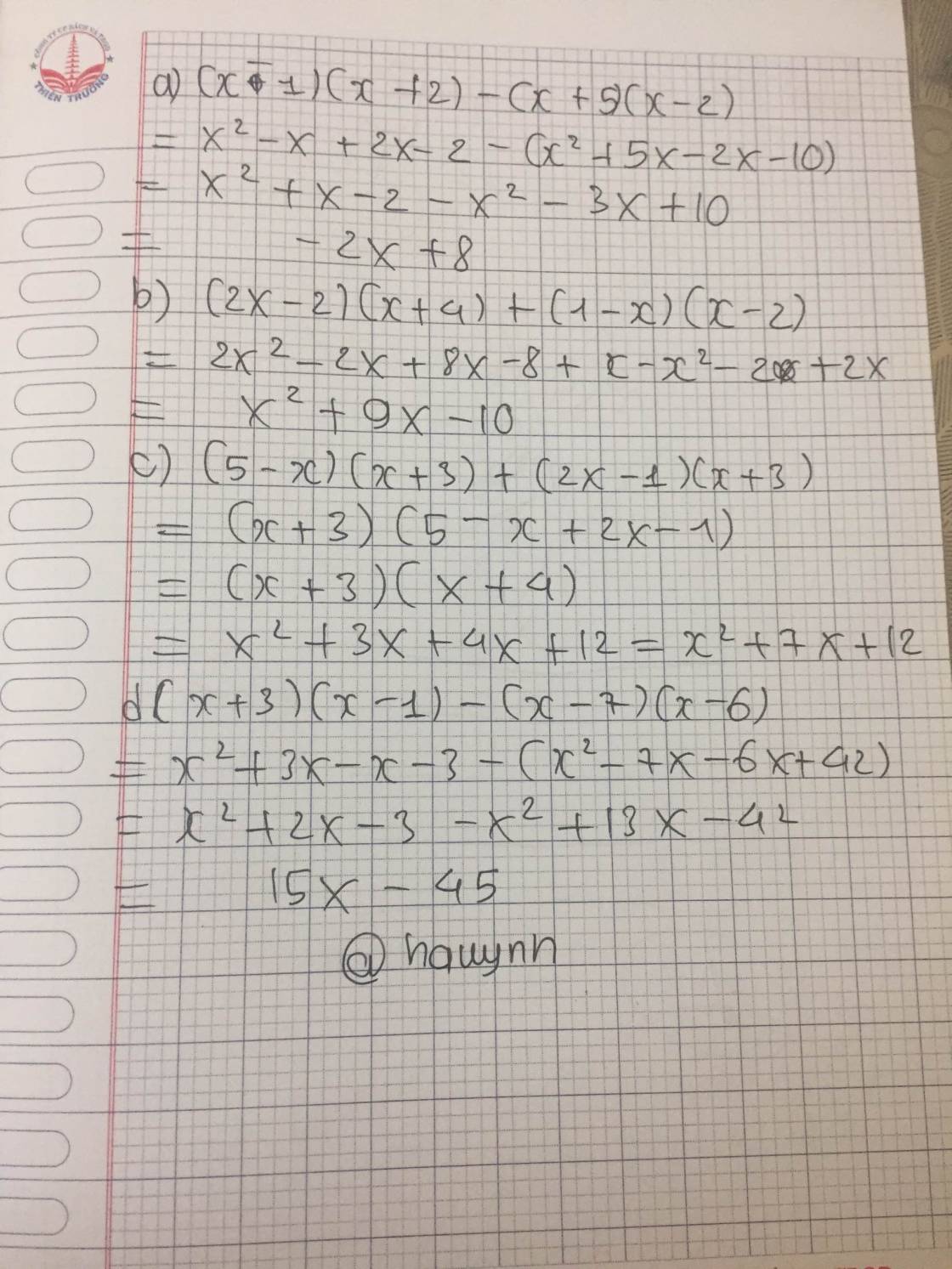
6:
a: Xét ΔABH vuông tại H có \(cosB=\dfrac{BH}{AB}\)
=>\(cosB=\dfrac{4}{16}=\dfrac{1}{4}\)
Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}\)
=>\(\dfrac{16}{BC}=\dfrac{1}{4}\)
=>BC=64(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=64^2-16^2=3840\)
=>\(AC=\sqrt{3840}=16\sqrt{15}\left(cm\right)\)
b: Xét ΔABN vuông tại A có AD là đường cao
nên \(BN\cdot BD=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BN\cdot BD=BH\cdot BC\)
A B C H 16 cm 4 cm N D