Cho tam giác ABC=DEF BIẾT B=50 ĐỘ D=70 ĐỘ.TÍNH SỐ ĐO GÓC C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 7 2023
ΔABC đồng dạng với ΔDEF
=>AB/DE=BC/EF=AC/DF=k=1/3
=>3/DE=4/DF=1/3
=>DE=9cm; DF=12cm
ΔABC đồng dạng với ΔDEF
=>góc B=góc E=60 độ; góc C=góc F=30 độ
góc A=góc D=180-60-30=90 độ
18 tháng 4 2022
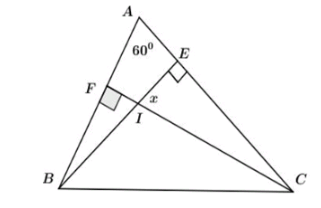
Câu 1 lỗi font còn câu 2 là 60 độ nhé do x và góc A đều bù góc FIE
18 tháng 4 2022
Bài 9: Cho tam giác DEF có D^ - F^ = 50° và E^ = 80°. Số đo của góc D^ và F^ lần lượt là?
XO
16 tháng 2 2021
Ta có\(\Delta ABC=\Delta DEF\)(1)
=> \(\hept{\begin{cases}AB=DE\\AC=DF\\BC=EF\end{cases}}\)(cạnh tương ứng) => EF = 8 cm
Tư (1) => \(\widehat{A}=\widehat{D}\)(góc tương ứng)
Lại có trong \(\Delta ABC\)có \(\widehat{A}+\widehat{B}+\widehat{C}=180^{\text{o}}\)
=> \(\widehat{A}+70^{\text{o}}+40^{\text{o}}=180^{\text{o}}\)
=> \(\widehat{A}=70^{\text{o}}\)
=> \(\widehat{D}=70^{\text{o}}\)
28 tháng 11 2021
\(\widehat{D}=180^0-\widehat{E}-\widehat{F}=50^0=\widehat{A}\\ \left\{{}\begin{matrix}AB=DE\\\widehat{A}=\widehat{D}\\AC=DE\end{matrix}\right.\Rightarrow\Delta ABC=\Delta DEF\left(c.g.c\right)\)
PT
5
20 tháng 2 2021
\(\Delta D\text{EF}\) cân tại D => \(\widehat{E}=\widehat{F}=50^o\)
Ta có: \(\widehat{D}+\widehat{E}+\widehat{F}=180^o\Rightarrow\widehat{D}=180^O-\widehat{E}-\widehat{F}=180^O-50^O-50^O=80^O\)
6 tháng 2 2022
Bài 1:
Số đo góc ngoài tại đỉnh C là \(74^0+47^0=121^0\)
Câu 2:
Đặt \(\widehat{D}=a;\widehat{E}=b\)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=52\\a+b=140\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=96\\b=44\end{matrix}\right.\)
Bài 3:
Theo đề, ta có: x+2x+3x=180
=>6x=180
=>x=30
=>\(\widehat{A}=30^0;\widehat{B}=60^0;\widehat{C}=90^0\)
22 tháng 11 2019
Xét t/giác DEF có \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\) (tổng 3 góc của 1 t/giác)
=> \(\widehat{D}=180^0-\widehat{E}-\widehat{F}=180^0-70^0-60^0=50^0\)
Xét t/giác ABC và t/giác DEF
có: AB = DE (gt)
AC = DF (gt)
\(\widehat{A}=\widehat{D}=50^0\)
=> t/giác ABC = t/giác DEF (c.g.c)
Do ∆ABC = ∆DEF (gt)
⇒ ∠A = ∠D = 70⁰
∆ABC có:
∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ABC)
⇒ ∠C = 180⁰ - (∠A + ∠B)
= 180⁰ - (70⁰ + 50⁰)
= 60⁰
ΔABC=ΔDEF
=>\(\widehat{A}=\widehat{D}=70^0\)
Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(\widehat{C}+70^0+50^0=180^0\)
=>\(\widehat{C}=180^0-120^0=60^0\)