 mấy câu gạch là mấy câu bỏ ý ạ giúp e phần này với ạ 🥲
mấy câu gạch là mấy câu bỏ ý ạ giúp e phần này với ạ 🥲
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e: \(\dfrac{x^2+3x+9}{x^3+4x^2+4x}\cdot\dfrac{x^2+2x}{x^3-27x}\)
\(=\dfrac{x^2+3x+9}{x\left(x^2+4x+4\right)}\cdot\dfrac{x\left(x+2\right)}{x\left(x^2-27\right)}\)
\(=\dfrac{x^2+3x+9}{\left(x+2\right)^2}\cdot\dfrac{x+2}{x\left(x^2-27\right)}\)
\(=\dfrac{\left(x^2+3x+9\right)}{\left(x+2\right)\cdot x\left(x^2-27\right)}\)
f: \(\dfrac{2x^2+4xy+2y^2}{5x-5y}\cdot\dfrac{15x-15y}{2x^3+2y^3}\)
\(=\dfrac{2\left(x^2+2xy+y^2\right)}{5\left(x-y\right)}\cdot\dfrac{15\left(x-y\right)}{2\left(x^3+y^3\right)}\)
\(=\dfrac{\left(x+y\right)^2}{1}\cdot\dfrac{3}{\left(x+y\right)\left(x^2-xy+y^2\right)}\)
\(=\dfrac{3\left(x+y\right)}{x^2-xy+y^2}\)
g: \(\dfrac{x^3-4x}{x^2-7x+12}\cdot\dfrac{x-4}{x^2-2x}\)
\(=\dfrac{x\left(x^2-4\right)}{\left(x-3\right)\left(x-4\right)}\cdot\dfrac{x-4}{x\left(x-2\right)}\)
\(=\dfrac{x^2-4}{\left(x-3\right)\left(x-2\right)}=\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-3\right)\left(x-2\right)}=\dfrac{x+2}{x-3}\)

4. \(x^2-3x+xy-3y=0\)
\(\Leftrightarrow x\left(x-3\right)+y\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-y\end{matrix}\right.\)
5. \(x^2-8x-3x+24=0\)
\(\Leftrightarrow x\left(x-8\right)-3\left(x-8\right)=0\)
\(\Leftrightarrow\left(x-8\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-8=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=3\end{matrix}\right.\)
6. \(\left(x-2\right)^2-5\left(2-x\right)=0\)
\(\Leftrightarrow\left(x-2\right)^2+5\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-2+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-2+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
7. \(3x\left(x-1\right)-x^2+2x-1=0\)
\(\Leftrightarrow3x\left(x-1\right)-\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow3x\left(x-1\right)-\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left[3x-\left(x-1\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{2}\end{matrix}\right.\)
8. \(x^2\left(x-3\right)+18-6x=0\)
\(\Leftrightarrow x^2\left(x-3\right)-6\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x^2-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\pm\sqrt{6}\end{matrix}\right.\)
10. \(\left(x-5\right)^2-\left(x-2\right)^2=0\)
\(\Leftrightarrow\left[\left(x-5\right)-\left(x-2\right)\right]\left[\left(x-5\right)+\left(x-2\right)\right]=0\)
\(\Leftrightarrow\left(x-5-x+2\right)\left(x-5+x-2\right)=0\)
\(\Leftrightarrow-3\left(2x-7\right)=0\)
\(\Leftrightarrow2x-7=0\)
\(\Leftrightarrow x=\dfrac{7}{2}\)
12. \(x^2\left(x-3\right)-4x+12=0\)
\(\Leftrightarrow x^2\left(x-3\right)-4\left(x-3\right)=0\)
\(\Leftrightarrow\left(x^2-4\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\)
14. \(3x^2-7x-10=0\)
\(\Leftrightarrow3x^2+3x-10x-10=0\)
\(\Leftrightarrow3x\left(x+1\right)-10\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\3x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{10}{3}\end{matrix}\right.\)
#Urushi
4: x^2-3x+xy-3y=0
=>x(x-3)+y(x-3)=0
=>(x-3)(x+y)=0
=>x=3 và x+y=0
=>x=3 và y=-3
6: (x-2)^2-5(2-x)=0
=>(x-2)^2+5(x-2)=0
=>(x-2)(x-2+5)=0
=>(x-2)(x+3)=0
=>x=-3 hoặc x=2
8: x^2(x-3)+18-6x=0
=>x^2(x-3)-6(x-3)=0
=>(x-3)(x^2-6)=0
=>x=3 hoặc \(x=\pm\sqrt{6}\)
10: (x-5)^2-(x-2)^2=0
=>(x-5-x+2)(x-5+x-2)=0
=>-3(2x-7)=0
=>2x-7=0
=>x=7/2
12: x^2(x-3)-4x+12=0
=>x^2(x-3)-4(x-3)=0
=>(x-3)(x^2-4)=0
=>(x-3)(x-2)(x+2)=0
=>\(x\in\left\{3;2;-2\right\}\)
14: 3x^2-7x-10=0
=>3x^2-10x+3x-10=0
=>(3x-10)(x+1)=0
=>x=10/3 hoặc x=-1



\(lim\dfrac{2\sqrt{7n^2-2n}}{3n+2}=lim\dfrac{2\sqrt{n^2\left(7-\dfrac{2}{n}\right)}}{3n+2}=lim\dfrac{2n\sqrt{7-\dfrac{2}{n}}}{n\left(3+\dfrac{2}{n}\right)}\)
\(=lim\dfrac{2\sqrt{7-\dfrac{2}{n}}}{3+\dfrac{2}{n}}=\dfrac{2\sqrt{7}}{3}\) \(=\dfrac{a\sqrt{7}}{b}\)
Suy ra : a/b = 2/3 => a - b = -1

\(\dfrac{x-1}{x+2}+\dfrac{6x}{x^2-4}=\dfrac{x+1}{2-x}\left(dkxd:x\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{x-1}{x+2}+\dfrac{6x}{\left(x-2\right)\left(x+2\right)}=-\dfrac{x+1}{x-2}\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)+6x+\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=0\)
\(\Leftrightarrow x^2-2x-x+2+6x+x^2+2x+x+2=0\)
\(\Leftrightarrow2x^2+6x+4=0\)
\(\Leftrightarrow2x^2+2x+4x+4=0\)
\(\Leftrightarrow2x\left(x+1\right)+4\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x+4\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+4=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{-1\right\}\)

III
1 Did you attend the Ban Flower Festival in Dien Bien last year?
2 Is Mua Sap a popular folk dance of the Thai people?
IV
1 They live in Wewbley, in north London
2 Her name is Tracy
3 No, there isn't
4 There are 4 people in his family
V
1 - B
2 - C
3 - d
4 - f
5 - a
6 - e
7 - g

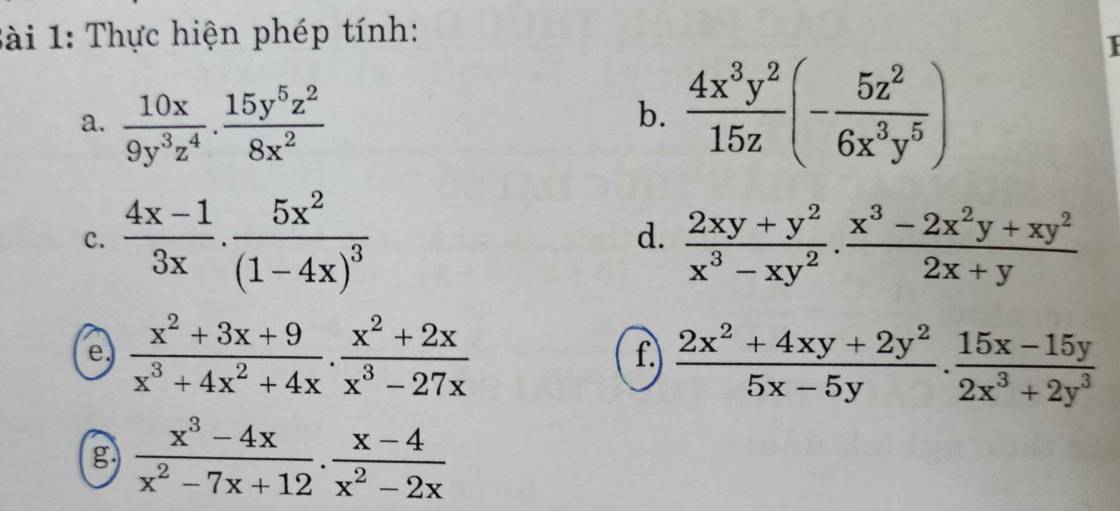



 ai giúp mình làm đống này với chỉ cần trả lời câu mấy ý mấy là được rồi ạ
ai giúp mình làm đống này với chỉ cần trả lời câu mấy ý mấy là được rồi ạ 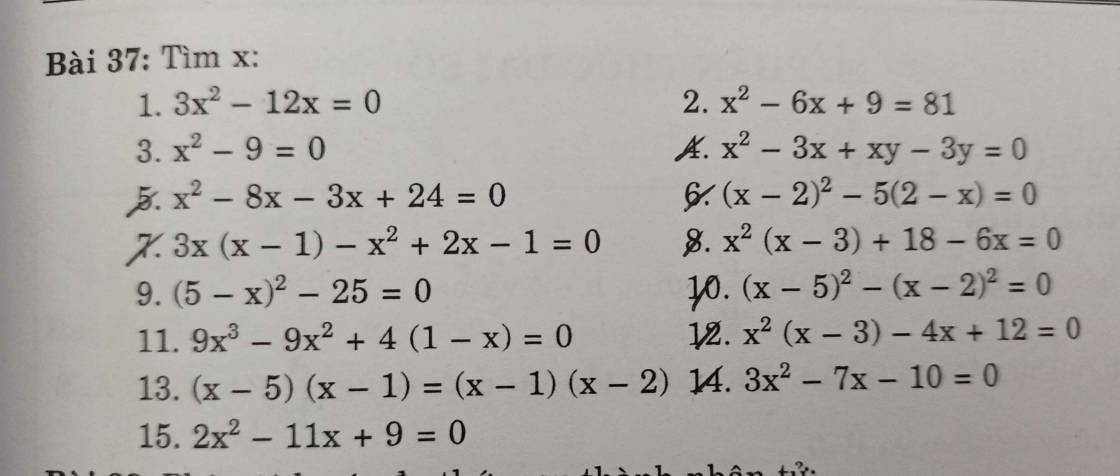



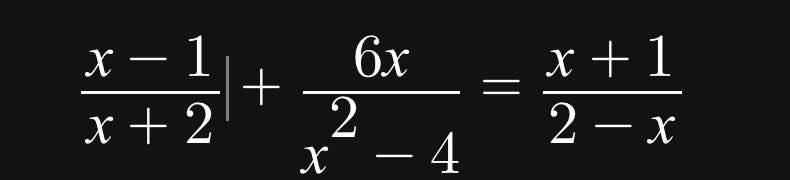


:)
1.B dynamite
2.B disappear
3.B refreshment
4.C disappointed
5.C division
6.C disappointment
7.B congratulate
8.D inedible
9.C congratulation
10.A oceanic
--thodagbun--
Tớ lm thêm cho bẹ tk :) á