cho ABC vuông tại A có AB=30cm.Kẻ AH vuông góc với BC.Biết AH=24cm,BC=50cm.Tính độ dài cạnh AC,BH và HC?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn đã hk định lí Pi-ta-go chưa ? Nếu hk rồi thì sau đây là cách giải:
tam giác ABH vuông tại H. Áp dụng định lí Pi-ta-go ta có:
AH2=AB2-BH2=52-32=16 => AH=4
Ta có: HC=BC-BH=8-3=5 =>HC=5
Tam giác AHC vuông tại H. Áp dụng định lí Pi-ta-go ta có:
AC2=AH2+HC2=42+52=41
Nếu có sai ở đâu thì sửa đi nhé !

1.
\(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\left(pytago\right)\)
Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=1,8\left(cm\right)\\CH=\dfrac{AC^2}{BC}=3,2\left(cm\right)\\AH=\sqrt{3,2\cdot1,8}=5,76\left(cm\right)\end{matrix}\right.\)
2.
Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=BH\cdot HC=HC\\AB^2=BH\cdot BC=BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}HC=4\left(cm\right)\\AB=\sqrt{HC+HB}=\sqrt{4+1}=\sqrt{5}\left(cm\right)\end{matrix}\right.\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-5}=2\sqrt{5}\left(cm\right)\)
Vậy \(AB=\sqrt{5}\left(cm\right);BC=5\left(cm\right);AC=2\sqrt{5}\left(cm\right)\)

a: \(AH=2\sqrt{6}\left(cm\right)\)
\(AB=2\sqrt{10}\left(cm\right)\)
\(AC=2\sqrt{15}\left(cm\right)\)

a) bạn tự vẽ hình nhé
sau khi kẻ, ta có AC=AH+HC=11
mà tam giác ABH vuông tại H
=> theo định lý Pytago => AH^2+BH^2=AB^2
=>BH=căn bậc 2 của 57
cũng theo định lý Pytago
=>BC^2=HC^2+BH^2
=>BC=căn bậc 2 của 66
b) bạn tự vẽ hình tiếp nha
ta có M là trung điểm của tam giác ABC => AM là đường trung tuyến của tam giác ABC vuông tại A
=>AM=MB=MC
theo định lý Pytago =>do tam giác HAM vuông tại H
=>HM^2+HA^2=AM^2
=>HM=9 => HB=MB-MH=32
=>AB^2=AH^2+HB^2 =>AB=căn bậc 2 của 2624
tương tự tính được AC=căn bậc 2 của 4100
=> AC/AB=5/4
CHÚC BẠN HỌC TỐT!!!

\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9^2+12^2}=15\left(cm\right)\)
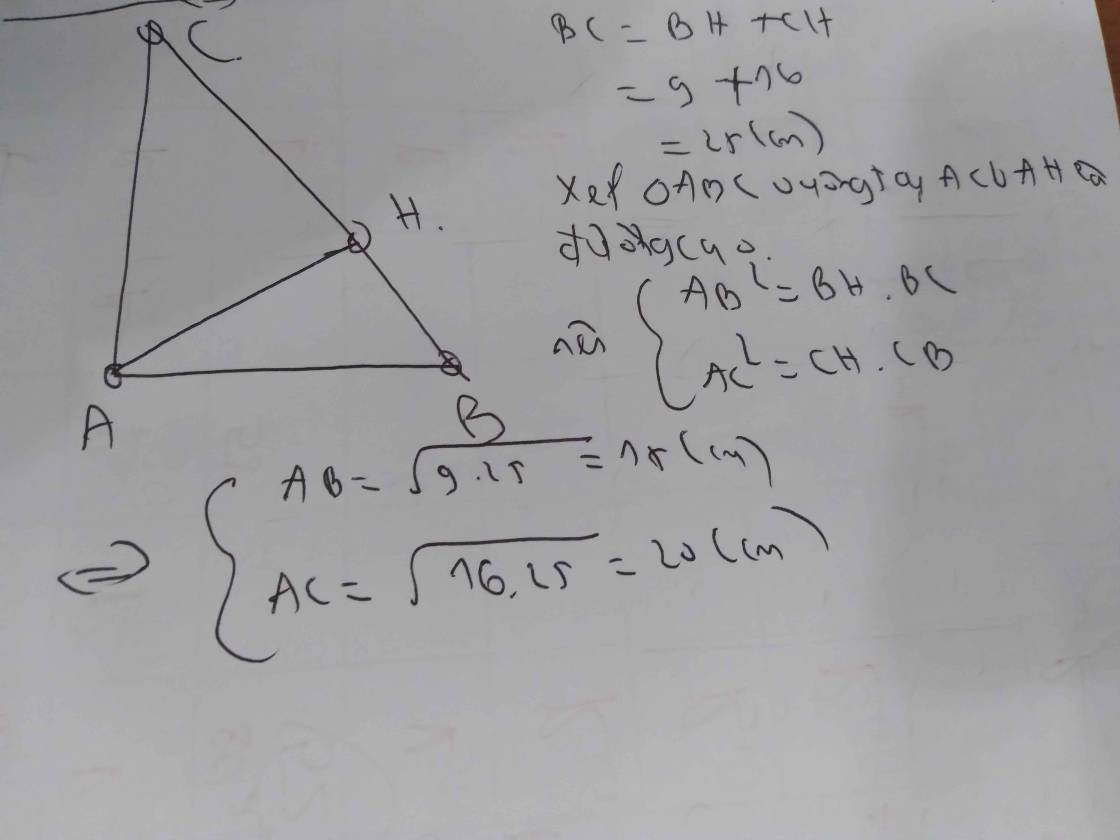
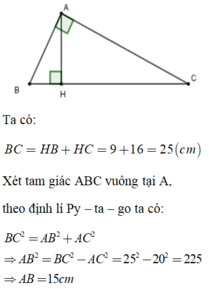
\(BC=BH+HC=9+16=25\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=15\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A

ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=50^2-30^2=1600\)
=>AC=40(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=HB\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(BH=\dfrac{30^2}{50}=18\left(cm\right);CH=\dfrac{40^2}{50}=32\left(cm\right)\)
Áp dụng định lý Pytago vào \(\Delta ABC\) vuông tại A ta có:
\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AB^2=50^2-30^2=1600\Rightarrow AC=\sqrt{1600}=40\left(cm\right)\)
Áp dụng định lý Pytago vào \(\Delta ABH\) vuông tại H ta có: \(AH^2+BH^2=AB^2\Rightarrow24^2+BH^2=30^2\Rightarrow BH^2=30^2-24^2=324\Rightarrow BH=\sqrt{324}=18\left(cm\right)\)\(HC=BC-BH=50-18=32\left(cm\right)\)