Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=15cm, BC=25cm.
a)tính AC,AH,HB,HC (câu này viết chắc đáp án thôi ạ)
b) Qua B kẻ đường thẳng d vuông góc với BC. Gọi I là trung điểm AH; CI cắt đường thẳng d tại K. Tính AK,BK
c) Gọi E là điểm đối xứng H qua A; BI cắt EC tại F. Chứng minh rằng tam giác EHC và tam giác BHI đồng dạng, I là trực tâm tam giác EBC
(NẾU ĐƯỢC THÌ VẼ HÌNH GIÚP MÌNH VỚI Ạ, KO VẼ CŨNG KHÔNG SAO)

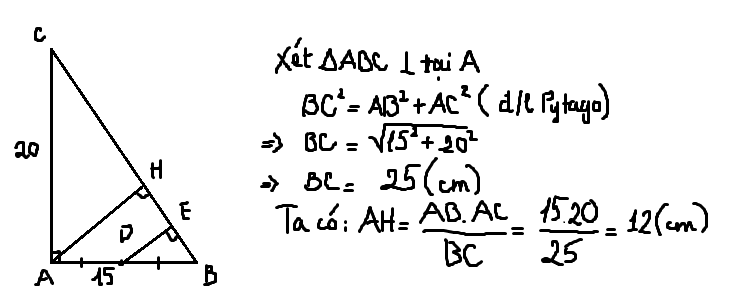
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=25^2-15^2=400\)
=>AC=20(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot25=15\cdot20=300\)
=>AH=12(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{15^2}{25}=9\left(cm\right)\\CH=\dfrac{20^2}{25}=16\left(cm\right)\end{matrix}\right.\)
b: I là trung điểm của AH
=>IA=IH=12/2=6cm
Xét ΔCBK có HI//BK
nên \(\dfrac{HI}{BK}=\dfrac{CH}{CB}\)
=>\(\dfrac{6}{BK}=\dfrac{16}{25}\)
=>\(BK=6\cdot\dfrac{25}{16}=9,375\left(cm\right)\)