32^60 và 81^50
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 10 2020
\(=\left(2^5\right)^{60}\)và \(\left(3^4\right)^{50}\)\(=2^{300}< 3^{200}\)
27 tháng 9 2020
ta có 32 mũ 60 bằng 4 mũ 2.5 tất cả 60 bằng 4 mũ 150
81 mũ 50 bằng 3 mũ 3 tất cả mũ 50 bằng 3 mũ 150
Suy ra 4 mũ 150 lớn hơn 3 mũ 150 hay 32 mũ 60 lớn hơn 81 mũ 50
NH
2
KN
1 tháng 10 2020
a. 536 và 1124
Ta có : 536 = ( 53 )12 = 12512
1124 = ( 112 )12 = 12112
Vì 12512 > 12112
nên 536 > 1124
b. 3260 và 8150
Ta có : 3260 = ( 25 )60 = 2300 = 8100
8150 = ( 34 )50 = 3200 = 9100
Vì 8100 < 9100
nên 3260 < 8150
CM
21 tháng 5 2019
Chọn A.
Dựa vào bảng đã cho ta có bảng phân bố tần số; tần suất như sau:
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
31 tháng 10 2023
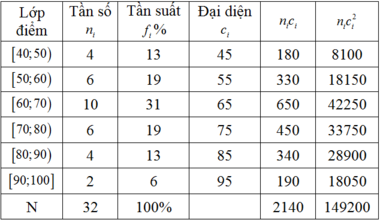
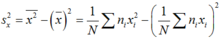
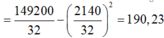
a/
\(27^{81}=\left(3^3\right)^{81}=3^{241}\)
\(81^{27}=\left(3^4\right)^{27}=3^{108}\)
\(\Rightarrow27^{81}=3^{241}>3^{108}=81^{27}\)
b/
\(5^{60}=\left(5^3\right)^{20}=125^{20}\)
\(7^{40}=\left(7^2\right)^{20}=49^{20}\)
\(\Rightarrow5^{60}=125^{20}>49^{20}=7^{40}\)
c/
\(11^{102}=\left(11^2\right)^{51}=121^{51}>121^{50}>99^{50}\)
26 tháng 10
d. So sánh a=12^34567 với b=(12^5)^12=12^60 => a>b
so sánh b=(12^5)^12 với c=34567^12 => b>c
Vậy a>c.
KV
3 tháng 12 2023
a) (38 - 60) + (20 - 38)
= 38 - 60 + 20 - 38
= (38 - 38) + (-60 + 20)
= 0 - 40
= -40
b) 75 - (20 + 75)
= 75 - 20 - 75
= (75 - 75) - 20
= 0 - 20
= -20
c) 32 + (60 - 32)
= 32 + 60 - 32
= (32 - 32) + 60
= 0 + 60
= 60
d) (81 - 36) - (81 - 36)
= 81 - 36 - 81 + 36
= (81 - 81) + (-36 + 36)
= 0 + 0
= 0
e) (2 + 4 + 6 + 8) - (1 + 3 + 5 + 7)
= 2 + 4 + 6 + 8 - 1 - 3 - 5 - 7
= (2 - 1) + (4 - 3) + (6 - 5) + (8 - 7)
= 1 + 1 + 1 + 1
= 4
f) (1 + 3 + 5 + 7 + ... + 99) - (2 + 4 + 6 + 8 + ... + 100)
= 1 + 3 + 5 + 7 + ... + 99 - 2 - 4 - 6 - 8 - ... - 100
= (1 - 2) + (3 - 4) + (5 - 6) + (7 - 8) + ... + (99 - 100)
= -1 - 1 - 1 - 1 - ... - 1 (50 chữ số 1)
= -50
H
4 tháng 2 2023
\(a,\dfrac{52}{32}=\dfrac{13}{8}\\ \dfrac{55}{65}=\dfrac{11}{13}\\ MSC:104\\ =>\dfrac{13}{8}=\dfrac{13.13}{8.13}=\dfrac{169}{104}\\ \dfrac{11}{13}=\dfrac{11.8}{13.8}=\dfrac{88}{104}\)
\(b,\dfrac{72}{64}=\dfrac{9}{8}\\ \dfrac{54}{81}=\dfrac{2}{3}\\ MSC:24\\ \dfrac{9}{8}=\dfrac{9.3}{8.3}=\dfrac{27}{24}\\ \dfrac{2}{3}=\dfrac{2.8}{3.8}=\dfrac{16}{24}\\ c,\dfrac{24}{36}=\dfrac{2}{3}\\ \dfrac{12}{30}=\dfrac{2}{5}\\ MSC:15\\ \dfrac{2}{3}=\dfrac{2.5}{3.5}=\dfrac{10}{15}\\ \dfrac{2}{5}=\dfrac{2.3}{3.5}=\dfrac{6}{15}\)
\(d,\dfrac{80}{40}=2\\ \dfrac{45}{63}=\dfrac{5}{7}\\ MSC:7\\ 2=\dfrac{14}{7}\\ e,\dfrac{150}{50}=3\\ \dfrac{100}{200}=\dfrac{1}{2}\\ MSC:2\\ 3=\dfrac{6}{2}\\ f,\dfrac{54}{81}=\dfrac{2}{3}\\ \dfrac{69}{93}=\dfrac{23}{21}\\ MSC:21\\ \dfrac{2}{3}=\dfrac{2.7}{3.7}=\dfrac{14}{21}\)
4 tháng 2 2023
\(a.\dfrac{52}{32}\text{=}\dfrac{13}{8};\dfrac{55}{65}\text{=}\dfrac{11}{13}\)
\(\dfrac{13.13}{13.8}\text{=}\dfrac{169}{104};\dfrac{11.8}{13.8}\text{=}\dfrac{88}{104}\)
\(c.\dfrac{24}{36}\text{=}\dfrac{2}{3};\dfrac{12}{30}\text{=}\dfrac{2}{5}\)
\(\dfrac{2.5}{3.5}\text{=}\dfrac{10}{15};\dfrac{2.3}{5.3}\text{=}\dfrac{6}{15}\)
\(b.\dfrac{72}{64}\text{=}\dfrac{9.3}{8.3}\text{=}\dfrac{27}{24};\dfrac{54}{81}\text{=}\dfrac{2.8}{3.8}\text{=}\dfrac{16}{24}\)
\(d.\dfrac{80}{40}\text{=}\dfrac{2.63}{63}\text{=}\dfrac{126}{63};\dfrac{45}{63}\)
\(e.\dfrac{150}{50}\text{=}\dfrac{3.2}{2}\text{=}\dfrac{6}{2};\dfrac{100}{200}\text{=}\dfrac{1}{2}\)
\(f.\dfrac{54}{81}\text{=}\dfrac{2.31}{3.31}\text{=}\dfrac{62}{93};\dfrac{69}{93}\)
Ta có:
\(32^{60}=\left(2^5\right)^{60}=2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(81^{50}=\left(9^2\right)^{50}=9^{100}\)
Mà: \(8< 9\)
\(\Rightarrow8^{100}< 9^{100}\)
\(\Rightarrow32^{60}< 81^{50}\)