Phương trình cos x= m - 4 có nghiệm khi và chỉ khi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
10 tháng 3 2018
Chọn B.
Xét hệ bất phương trình:
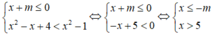
Để hệ bất phương trình có nghiệm thì 5 < -m ⇔ m > -5.
CM
14 tháng 8 2019
Đáp án D
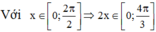
dựa vào đường tròn lượng giác suy ra PT có đúng hai nghiệm khi
CM
10 tháng 4 2018
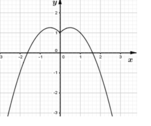
x + 1 = x 2 + m ⇔ m = f x = − x 2 + x + 1 k h i x ≥ 0 − x 2 − x + 1 k h i x < 0
Biểu diễn đồ thị hàm số f(x) lên hệ trục tọa độ như hình vẽ bên trên:
+ Vẽ đồ thị hàm số y = - x 2 + x + 1
+ Giữ nguyên nhánh đồ thị bên phải trục tung và lấy đối xứng nó qua trục tung.
+ Xóa bỏ phần bên trái trục tung trước đó đi.
Dựa vào đồ thị ta suy ra không tồn tại m để phương trình m = f x có duy nhất 1 nghiệm.
Đáp án cần chọn là: D
CM
3 tháng 1 2017
Chọn C.
Xét phương trình: x 2 - (m + 1)x + 1 = 0
Ta có: Δ = (m + 1 ) 2 - 4.1.1 = m 2 - 2m + 1 - 4 = m 2 - 2m - 3
Phương trình x 2 - (m + 1)x + 1 = 0 có nghiệm
⇔ Δ ≥ 0 ⇔
m
2
- 2m - 3 ≥ 0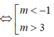 
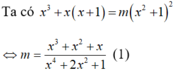
CM
2 tháng 10 2017
Xét hàm số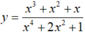 
xác định trên R.
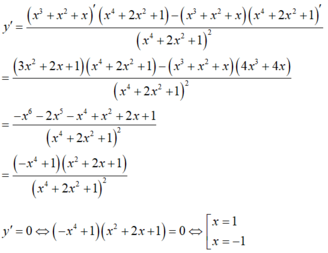
Bảng biến thiên
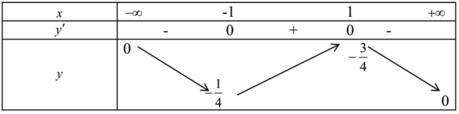
Phương trình (1) có nghiệm thực khi đường thẳng y= m cắt đồ thị hàm số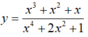 
Khi và chỉ khi -1/4 ≤ m≤ 3/4
Chọn D.
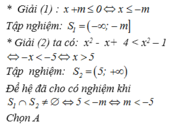
Phương trình \(\cos x=m-4\) khi và chỉ khi \(-1\le m-4\le1\) \(\Leftrightarrow3\le m\le5\)