Cho tam giác MNP cân tại M, điểm Q nằm giữa M và N, lấy điểm E nằm giữa M và P sao cho MQ=PE. Từ Q, kẻ đường thẳng song song MP cách NP ở E. CM rằng
a) tứ giác MQEF là hình bình hành
b) trung điểm MF thuộc đường thẳng QE
( có vẽ hình )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề:
Cho tam giác MNP cân tại M, điểm Q nằm giữa M và N, lấy điểm E nằm giữa M và P sao cho MQ = PE. Từ Q kẻ đường thẳng song song MP cách NP ở F. Chứng minh:
a) Tứ giác MQFE là hình bình hành
b) Trung điểm của MF thuộc đường thẳng QE
GIẢI
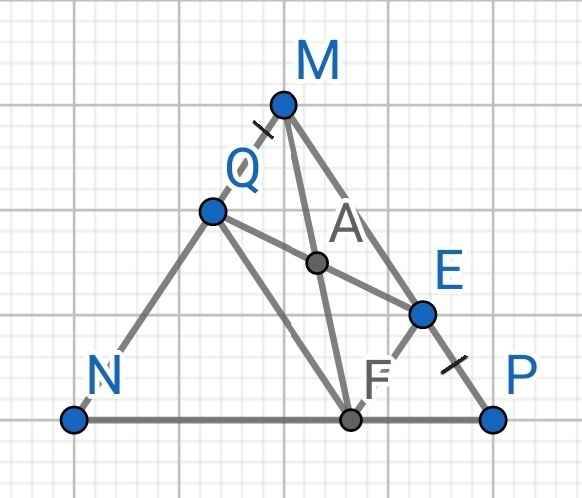
a) Do ∆MNP cân tại M (gt)
⇒ MN = MP
Mà MQ = PE (gt)
⇒ MN - MQ = MP - ME
⇒ QN = ME
Do QF // MP (gt)
⇒ ∠QFN = ∠MPN (đồng vị) (1)
Mà ∆MNP cân tại M
⇒ ∠MPN = ∠MNP
⇒ ∠MPN = ∠QNF (2)
Từ (1) và (2) ⇒ ∠QFN = ∠QNF
⇒ ∆QNF cân tại Q
⇒ QN = QF
Mà QN = ME (cmt)
⇒ QF = ME
Do QF // MP (gt)
⇒ QF // ME
Tứ giác MQFE có:
QF // ME (cmt)
QF = ME (cmt)
⇒ MQFE là hình bình hành
b) Gọi A là trung điểm của MF
Do MQFE là hình bình hành
⇒ A là trung điểm của hai đường chéo MF và QE
⇒ A là trung điểm của QE
⇒ A ∈ QE

tự kẻ hình nha
a) Vì M là trung điểm AB, PM=MQ, P,M,Q thẳng hàng=> M là trung điểm PQ
=>PQ giao AB tại trung điểm mỗi đường=> APBQ là hbh mà AB vuông góc với PQ=> APBQ là hình thoi
b) vì APBQ là hình thoi=> PB//AQ mà PB//CE=> CE//AQ (1)
ta có PQ vuông góc với AB
AC vuông góc với AB
=> AC//PQ=> EQ//AC ( PQ cắt đường thẳng // với PB tại E=> E thuộc PQ)(2)
từ (1);(2)=> ACEQ là hbh
c) 1) trong tam giác ABC có
MN //AC( N thuộc MP)
AM=MB
=> MN là đtb của tam giác => MN=AC/2=> AC=2MN
2) Vì AC=2MN=> AC=6cm
MN là đtb=> CN=BN
tam giác ABC vuông tại A
=> AN=BN=CN=BC/2( tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
=> BC=2AN=10cm
vì tam giác ABC vuông tại A=> AB^2+AC^2=BC^2
=> AB^2=100-36
=> AB=8 (AB>0)
=> chu vi tam giác ABC là 6+8+10=24(cm)

bạn tự vẽ hình nha!Nên sửa DQEF thành DQEP.
a,tứ giác DQEP có:ME=MD,MQ=MP nên DQEP là hình bình hành.
Lại có:DE vuông góc với QP nên hình bình hành DQEP là hình thoi.
b,DQEP là hình thoi nên EP song song với DQ mà FK song song với PE nên DQ song song với FK(1)
Lại có:DF và QK cùng vuông góc với DM nên DF song song với QK(2).
Từ (1) và (2) suy ra DFKQ là hình bình hành

a, xét tma giác MNE và tam giác MPE có :
MN = MP và góc MNE = góc MPE do tam giác MNP cân tại M (Gt)
NE = EP do E là trđ của NP (gt)
=> tam giác MNE = tam giác MPE (c-g-c)
=> góc MEN = góc MEP (đn)
mà góc MEN + góc MEP = 180 (kb)
=> góc MEN = 90
=> MN _|_ NP và có M là trđ của PN (Gt)
=> ME là trung trực của NP (đn)
b, xét tam giác MKE và tam giác MHE có : ME chung
góc NME = góc PME do tam giác MNE = tam giác MPE (Câu a)
góc MKE = góc MHE = 90
=> tam giác MKE = tam giác MHE (ch-cgv)
=> MK = MH (đn)
=> tam giác MHK cân tại M (đn)
=> góc MKH = (180 - góc NMP) : 2 (tc)
tam giác MNP cân tại M (Gt) => góc MNP = (180 - góc NMP) : 2 (tc)
=> góc MKH = góc MNP mà 2 góc này đồng vị
=> KH // NP (đl)
Sửa đề:
Cho tam giác MNP cân tại M, điểm Q nằm giữa M và N, lấy điểm E nằm giữa M và P sao cho MQ = PE. Từ Q kẻ đường thẳng song song MP cách NP ở F. Chứng minh:
a) Tứ giác MQFE là hình bình hành
b) Trung điểm của MF thuộc đường thẳng QE
GIẢI
a) Do ∆MNP cân tại M (gt)
⇒ MN = MP
Mà MQ = PE (gt)
⇒ MN - MQ = MP - ME
⇒ QN = ME
Do QF // MP (gt)
⇒ ∠QFN = ∠MPN (đồng vị) (1)
Mà ∆MNP cân tại M
⇒ ∠MPN = ∠MNP
⇒ ∠MPN = ∠QNF (2)
Từ (1) và (2) ⇒ ∠QFN = ∠QNF
⇒ ∆QNF cân tại Q
⇒ QN = QF
Mà QN = ME (cmt)
⇒ QF = ME
Do QF // MP (gt)
⇒ QF // ME
Tứ giác MQFE có:
QF // ME (cmt)
QF = ME (cmt)
⇒ MQFE là hình bình hành
b) Gọi A là trung điểm của MF
Do MQFE là hình bình hành
⇒ A là trung điểm của hai đường chéo MF và QE
⇒ A là trung điểm của QE
⇒ A ∈ QE