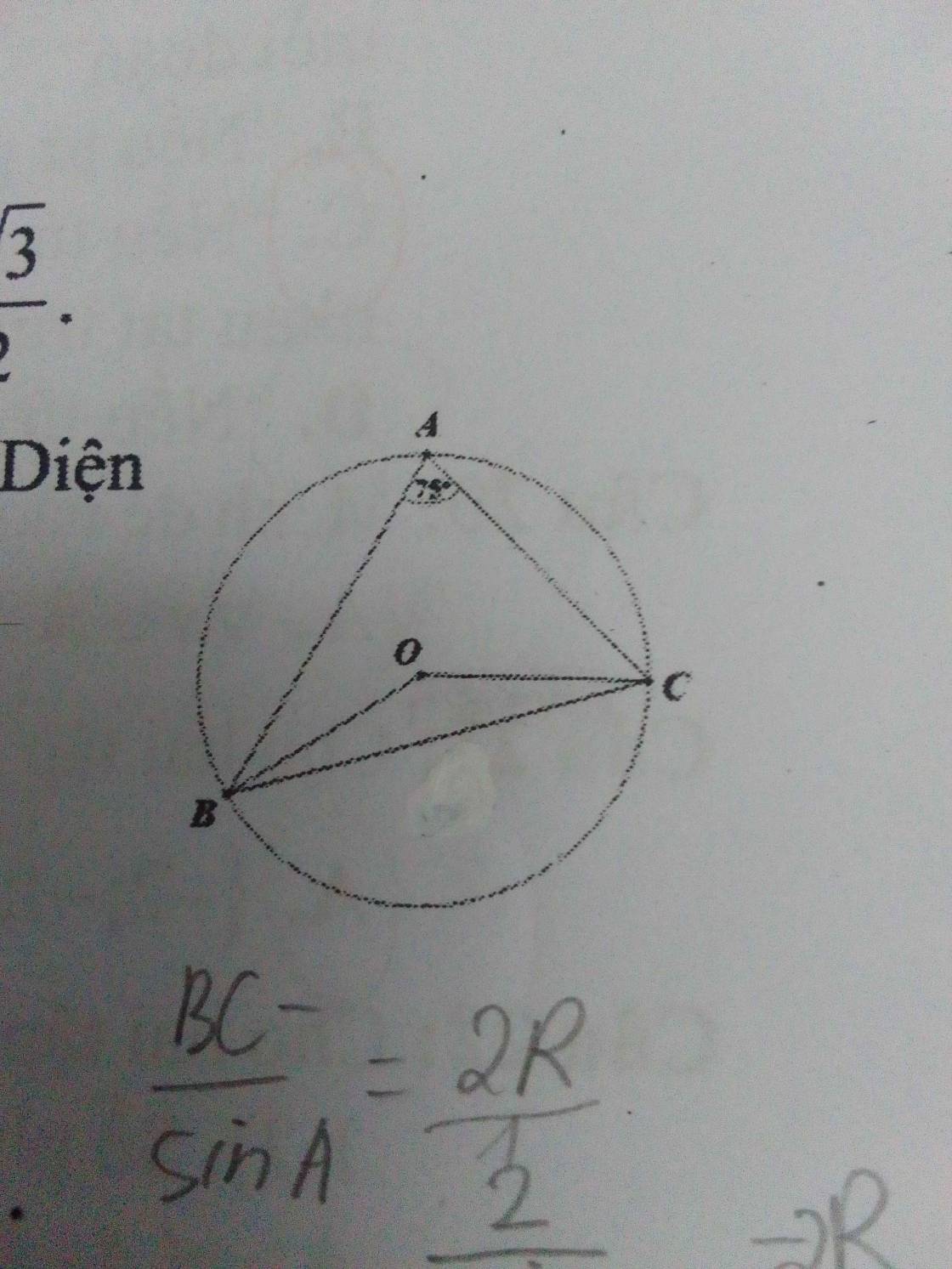 Cho tam giác ABC, góc A=75° nội tiếp đường tròn tâm O bán kính R=1. tính diện tích tam giác OBC.
Cho tam giác ABC, góc A=75° nội tiếp đường tròn tâm O bán kính R=1. tính diện tích tam giác OBC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2

Đáp án A.
Áp dụng định lý Sin, ta có 2 R = A B sin A C B ^ ⇒ A B = 2 R . sin 60 ° = R 3 .
Và 2 R = B C sin B A C ^ ⇒ B C = 2 3 + 1 2 . Xét ∆ B H C vuông tại H, ta có
sin A C B ^ = B H B C ⇒ B H = sin 60 ° . B C = 6 + 3 2 4 R .
cos A C B ^ = C H B C ⇒ C H = cos 60 ° . B C = 6 + 2 4 R .
Khi quay ∆ B H C quanh trục AC ta được hình nón tròn xoay có bán kính đường tròn đáy r = BH và chiều cao h = C H = 6 + 2 4 R . Vậy S x q = πrl = 3 + 2 3 2 πR 2

\(\widehat{BAC}=60^o\Rightarrow\widehat{BOC}=120^o\). Diện tích cần tìm là \(\pi\).32-1/2.3.3.sin120o=9\(\pi\)-9\(\sqrt{3}\)/4 (cm2)\(\approx\)24,38 (cm2).
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot\widehat{BOC}\)
=>\(\widehat{BOC}=75^0:\dfrac{1}{2}=150^0\)
Diện tích tam giác OBC là:
\(S_{OBC}=\dfrac{1}{2}\cdot OB\cdot OC\cdot sinBOC\)
\(=\dfrac{1}{2}\cdot1\cdot1\cdot sin150=\dfrac{1}{4}\)