giải hpt:
√x + √y = 4
√x + 5 + √y + 5 = 6;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
29 tháng 12 2021
\(\left\{{}\begin{matrix}\dfrac{7}{\sqrt{x}-7}-\dfrac{4}{\sqrt{y}+6}=\dfrac{5}{3}.\\\dfrac{5}{\sqrt{x}-7}+\dfrac{3}{\sqrt{y}+6}=2\dfrac{1}{6}.\end{matrix}\right.\) \(\left(x,y\ge0;x\ne49\right).\)
\(\Leftrightarrow\left\{{}\begin{matrix}7\dfrac{1}{\sqrt{x}-7}-4\dfrac{1}{\sqrt{y}+6}=\dfrac{5}{3}.\\5\dfrac{1}{\sqrt{x}-7}+3\dfrac{1}{\sqrt{y}+6}=\dfrac{13}{6}.\end{matrix}\right.\)
Đặt \(\dfrac{1}{\sqrt[]{x}-7}=a\); \(\dfrac{1}{\sqrt[]{y}+6}=b\left(a,b\ne0\right).\)
\(\Rightarrow\left\{{}\begin{matrix}7a-4b=\dfrac{5}{3}.\\5a+3b=\dfrac{13}{6}.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{3}.\\b=\dfrac{1}{6}.\end{matrix}\right.\) \(\left(TM\right).\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{\sqrt{x}-7}=\dfrac{1}{3}.\\\dfrac{1}{\sqrt{y}+6}=\dfrac{1}{6}.\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}-7=3.\\\sqrt{y}+6=6.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=10.\\\sqrt{y}=0.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=100\left(TM\right).\\y=0\left(TM\right).\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm duy nhất là: \(\left(x;y\right)=\left(100;0\right).\)
HN
0
14 tháng 2 2022
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3.4}{x+y}+\dfrac{3.4}{x-y}=\dfrac{5}{2}\\\dfrac{4}{x+y}+\dfrac{2.4}{x+y}=\dfrac{4}{3}\end{matrix}\right.\\ Đặt.a=\dfrac{4}{x+y},b=\dfrac{4}{x-y}\\ \Leftrightarrow\left\{{}\begin{matrix}3a+3b=\dfrac{5}{2}\\a+2b=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a+3b=\dfrac{5}{2}\\3a+6b=4\end{matrix}\right.\)
\(\Leftrightarrow\left(3a+6b\right)-3a-3b=4-\dfrac{5}{2}\\ \Leftrightarrow3b=\dfrac{3}{2}\Rightarrow b=\dfrac{1}{2}\Rightarrow a+2.\dfrac{1}{2}=\dfrac{4}{3}\\\Leftrightarrow a+1=\dfrac{4}{3}\Rightarrow a=\dfrac{1}{3}\\ \Rightarrow\left\{{}\begin{matrix}\dfrac{4}{x+y}=\dfrac{1}{3}\\\dfrac{4}{x+y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=12\\x-y=8\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=10\\y=2\end{matrix}\right.\)
28 tháng 5 2018
<=>
2/(x+y)+3√(x-2)=7(*)
5/(x+y)-2√(x-2)=1-5/2=-3/2(**)
(*).5-(**).2
(15+4)√(x+2)=35+3=38
√(x-2)=2; x=6
2/(x+y)=1; => y=2-x=-4
(x,y)=(6,-4)
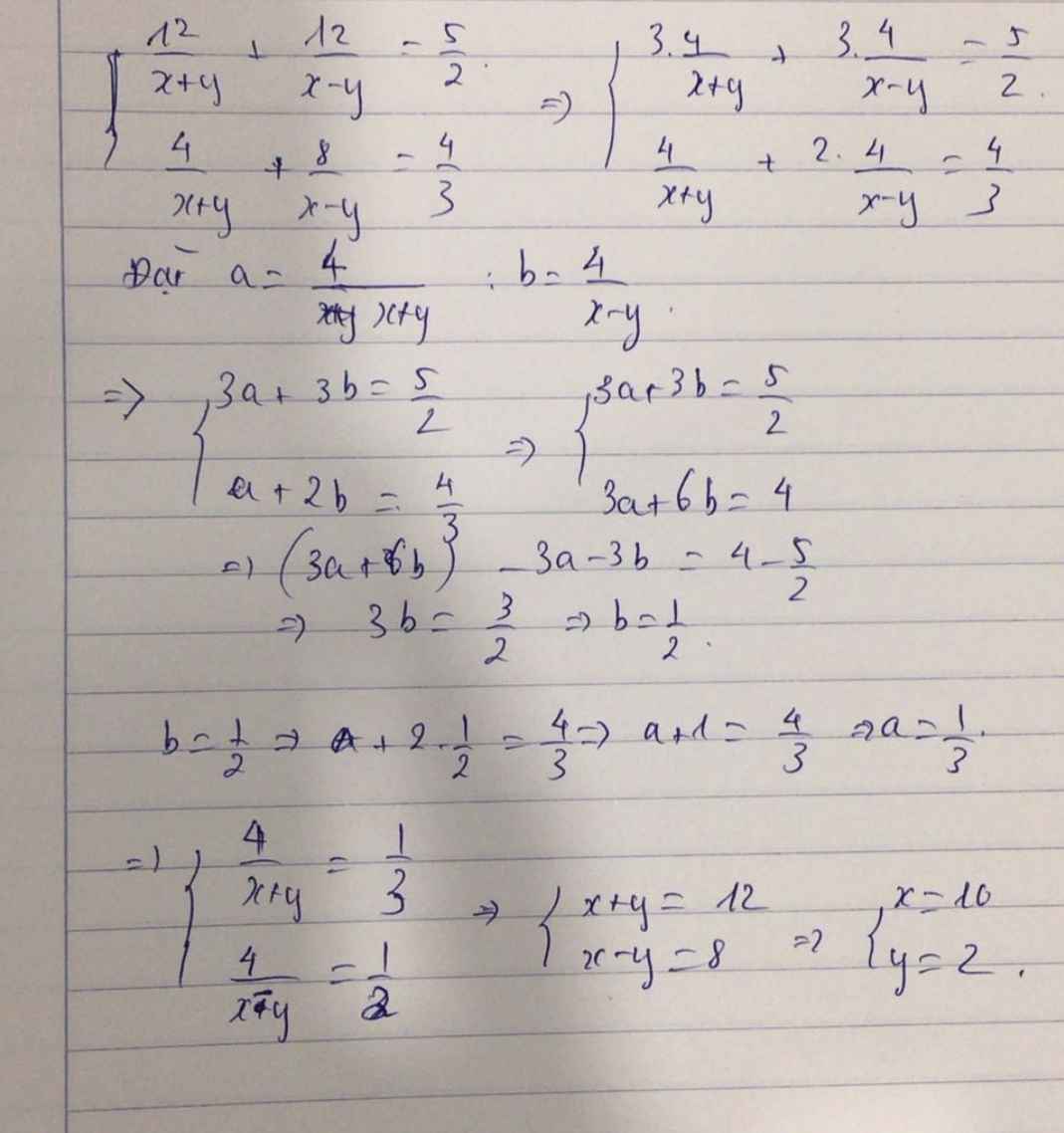
Đk \(x;y\ge0\)
Ta có hệ \(\hept{\begin{cases}\sqrt{x}+\sqrt{y}=4\left(1\right)\\\sqrt{x+5}+\sqrt{y+5}=6\left(2\right)\end{cases}}\)
Từ (1) ta có \(\sqrt{x}+\sqrt{y}=4\Rightarrow x+y+2\sqrt{xy}=16\Rightarrow x+y=16-2\sqrt{xy}\)
Từ (2) ta có \(\sqrt{x+5}+\sqrt{y+5}=6\Rightarrow x+5+y+5+2\sqrt{\left(x+5\right)\left(y+5\right)}=36\)
\(\Rightarrow16-2\sqrt{xy}+10+2\sqrt{\left(x+5\right)\left(y+5\right)}=36\)
\(\Leftrightarrow2\sqrt{\left(x+5\right)\left(y+5\right)}=10+2\sqrt{xy}\)
\(\Leftrightarrow4\left(xy+5x+5y+25\right)=100+40\sqrt{xy}+4xy\)
\(\Leftrightarrow x+y-2\sqrt{xy}=0\Leftrightarrow\sqrt{x}=\sqrt{y}\Leftrightarrow x=y\)
\(\Rightarrow\sqrt{x}+\sqrt{x}=4\Leftrightarrow x=4\Rightarrow y=4\)
Vậy hệ có nghiệm \(\left(x;y\right)=\left(4;4\right)\)