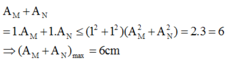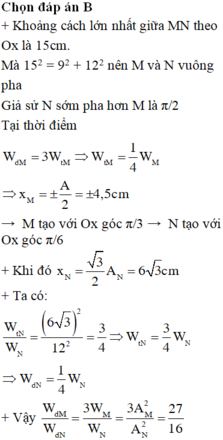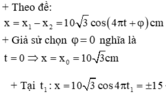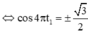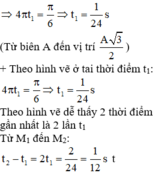Hai chất điểm dao động điều hòa trên 2 đường thẳng song song kề nhau và song song với trục Ox. Vị trí cân bằng của chúng nằm trên cùng 1 đường thẳng qua gốc O và vuông góc với trục Ox. Phương trình dao động \(x_1=4cos\left(4\pi t+\dfrac{\pi}{3}\right)cm; x_2=4\sqrt{2}cos\left(4\pi t+\dfrac{\pi}{12}\right)cm\). Thời điểm lần thứ 2020 khoảng cách giữa 2 chất điểm theo phương Ox đạt giá trị cực đại kể từ thời điểm ban đầu là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
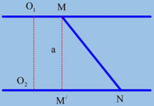
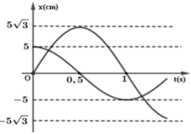
Khoảng cách giữa hai chất điểm là độ dài của đoạn MN
M N = M M ' 2 + M ' N 2 = a 2 + Δ x 2 1
Trong đó:
MM': Khoảng cách giữa hai đường thẳng
M'N: Khoảng cách giữa hai chất điểm tính trên phương dao động trùng phương Ox:
M
'
N
=
Δ
x
Từ (1) ta có: M N max khi Δ x max = A 1 2 + A 2 2 = 5 3 2 + 5 2 = 10 c m (hai dao động vuông pha)
Vậy M N max = 8 2 + 10 2 = 12 , 8 c m

Đáp án D
Theo giả thiết bài toán, ta có:
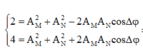
![]()
Áp dụng bất đẳng thức Bunhia cho biểu thức trên
![]()
![]()

Đáp án D
Theo giả thiết bài toán, ta có:
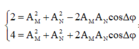
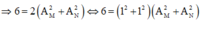
Áp dụng bất đẳng thức Bunhia cho biểu thức trên
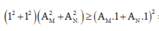
![]()

Giải thích: Đáp án D
Phương pháp: Sử dụng lí thuyết về tổng hợp hai dao động điều hòa cùng tần số kết hợp với bất đẳng thức Bu-nhi-a-cốp-xki để đánh giá
Cách giải:
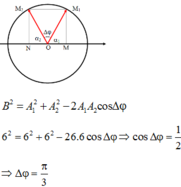
Giả sử phương trình dao động của M và N lần lượt là 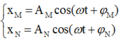
Biên độ dao động tổng hợp của hai dao động trên là: ![]()
Khoảng cách lớn nhất của M và N trên phương Ox là: ![]()
Theo đề bài ta có: 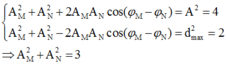
Thấy rằng: