Giải hệ phương trình
\(x^2+xy+y=-0,35\)
\(xy+3x-5y=-38,3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 1 2018
Cách 1
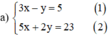
Từ (1) ta rút ra được y = 3x – 5 (*)
Thế (*) vào phương trình (2) ta được :
5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.
Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.
Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).
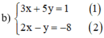
Từ (2) ta rút ra được y = 2x + 8 (*)
Thế (*) vào phương trình (1) ta được :
3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.
Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.
Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).
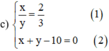
Từ (1) ta rút ra được x = 2 3 y (*)
Thế (*) vào phương trình (2) ta được :
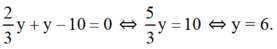
Thay y = 6 vào (*) ta được x = 4.
Vậy hệ phương trình có nghiệm duy nhất (x ; y) = (4 ; 6).
Cách 2
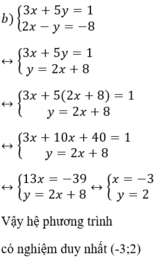
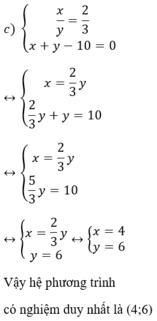
Kiến thức áp dụng
+ Giải hệ phương trình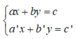 
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.
KT
28 tháng 7 2018
Viết lại phương trình thứ 2 của hệ thành:
\(\hept{\begin{cases}x^2+x\left(y-3\right)+y^2-4y+4=0\\y^2+y\left(x-4\right)+x^2-3x+4=0\end{cases}}\) \(\Leftrightarrow\)\(\hept{\begin{cases}\Delta_x\ge0\\\Delta_y\ge0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}1\le y\le\frac{7}{3}\\0\le x\le\frac{4}{3}\end{cases}}\)
Thế \(xy=-x^2-y^2+3x+4y-4\)từ pt (2) vào pt (1) ta được:
\(3x^3+18x^2+45x-3y^3+3y^2+8y-108=0\)
- Xét hàm số: \(f\left(x\right)=3x^3+18x^2+45x\)trên \(\left[0;\frac{4}{3}\right]\)ta có: \(f'\left(x\right)=9x^2+6x+45>0\)
nên hàm số f(x) đồng biến. suy ra: \(f\left(x\right)\le f\left(\frac{4}{3}\right)=\frac{892}{9}\)
- Xét hàm số: \(g\left(y\right)=-3y^3+3y^2+8y-108\)trên \(\left[0;\frac{7}{3}\right]\)ta có: \(g'\left(y\right)=-9y^2+6y+8,\)
\(g'\left(y\right)=0\)\(\Leftrightarrow\)\(y=\frac{4}{3}\) suy ra: \(g\left(y\right)\le g\left(\frac{4}{3}\right)=\frac{-892}{0}\)
suy ra: \(f\left(x\right)+g\left(y\right)\le0\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y=\frac{4}{3}\)
thử lại thấy đúng
nên cặp nghiệm \(\left(x;y\right)=\left(\frac{4}{3};\frac{4}{3}\right)\)thỏa mãn hệ
p/s: chúc bạn học tốt, cách này đối vs bạn chắc khó hiểu, có j thì hỏi thầy cô dạy cho dễ hiểu nha hoặc ib mk (nhưng mk mak giải thích thì chắc bạn khó hiểu hơn ^^ ko có khiếu ăn nói)
NH
2
ML
29 tháng 7 2016
\(\hept{\begin{cases}x^2+y^2+xy=3\\xy+3x^2=4\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}4\left(x^2+y^2+xy\right)=3\left(3x^2+xy\right)\text{ }\left(\text{1}\right)\\3x^2+xy=4\end{cases}}\)
\(\left(1\right)\Leftrightarrow5x^2-xy-4y^2=0\Leftrightarrow\left(x-y\right)\left(5x+4y\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}x-y=0\\5x+4y=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}y=x\\y=-\frac{5}{4}x\end{cases}}\)
\(\text{TH1:}y=x\), ta được hệ \(\hept{\begin{cases}x=y\\3x^2+xy=4\end{cases}}\)
TH2: \(y=-\frac{5}{4}x\), ta có hệ \(\hept{\begin{cases}y=-\frac{5}{4}x\\3x^2+xy=4\end{cases}}\)
27 tháng 2 2022
Xét \(y=0\)\(\Rightarrow...\)
Xét \(y\ne0\). Ta có:
\(\left\{{}\begin{matrix}x^2+y^2+xy+2x=5y\\\left(x^2+2x\right)\left(x+y-3\right)=-3y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+2x=5y-y^2-xy\left(1\right)\\\left(x^2+2x\right)\left(x+y-3\right)=-3y\left(2\right)\end{matrix}\right.\)
Thay (1) vào (2), ta có:
\(\left(5y-y^2-xy\right)\left(x+y-3\right)=-3y\)
\(-y\left(x+y-5\right)\left(x+y-3\right)=-3y\)
\(\Leftrightarrow\left(x+y-5\right)\left(x+y-3\right)=3\left(\cdot\right)\)
Đặt \(x+y-5=t\), phương trình \(\left(\cdot\right)\) trở thành
\(t\left(t+2\right)=3\)\(\Leftrightarrow t^2+2t+1=4\Leftrightarrow\left(t+1\right)^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}t+1=2\\t+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}t=1\\t=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y-5=1\\x+y-5=-3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+y=6\\x+y=2\end{matrix}\right.\)\(\Rightarrow...\)
4 tháng 9 2016
ban dua cau hoi naylen 24h de duoc hoi dap tot hon nha
hệ phương trình mik chưa bít nhưng mik có 1 cách ~~ ko phải hệ phương trình