cho hình tứ diện ABCD. Gọi M là điểm trên cạnh AD sao cho MA = 2MD
a, G là trọng tâm tam giác ABD. Chứng minh rằng: MG // (BCD)
b, H là trọng tâm tam giác ABC. Chứng minh rằng: HG // (BCD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 4 2017
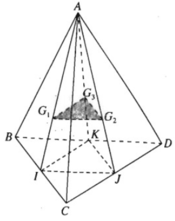
Gọi I, J và K lần lượt là trung điểm của các cạnh BC, CD và BD. Theo tính chất trọng tâm của tam giác ta có:
22 tháng 9 2023
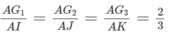
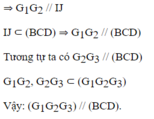
Tham khảo:
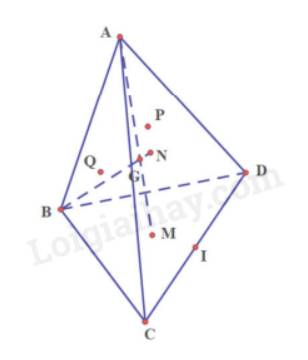
a) Ta có: M là trọng tâm của tam giác BCD
Nên M nằm trên trung tuyến BI (1)
Ta có: N là trọng tâm của tam giác ACD
Nên N nằm trên trung tuyến AI (2)
Từ (1) và (2) suy ra M và N thuộc mp (ABI)
b) Gọi H, K lần lượt là trung điểm của AG, BG
Ta có: HK // AB
AB // MN
Suy ra MN // HK
Theo định lý Ta-let, ta có: \(\frac{{GM}}{{GH}} = \frac{{GN}}{{GK}} = \frac{{MN}}{{HK}}(1)\)
Ta có:\(\frac{{HK}}{{AB}} = \frac{1}{2},\frac{{MN}}{{AB}} = \frac{1}{3}\)
Do đó \(\frac{{MN}}{{AB}}:\frac{{HK}}{{AB}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{HK}} = \frac{2}{3}(2)\)
Từ (1) và (2) suy ra\(\frac{{GM}}{{GH}} = \frac{2}{3}GH = \frac{1}{2}GA \Rightarrow \frac{{GM}}{{\frac{1}{2}GA}} = \frac{2}{3} \Rightarrow \frac{{GM}}{{GA}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GN}}{{GB}} = \frac{1}{3}\)
c) Gọi H, K lần lượt là trung điểm của BC, BD
Tam giác AHD có:\(\frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Suy ra: QM // AD
Do đó, tam giác QGM đồng dạng với tam giác DGA
Nên D, G, Q thẳng hàng
Ta có: QM // AD nên \(\frac{{QM}}{{AD}} = \frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Mà \(\frac{{QM}}{{AD}} = \frac{{QG}}{{GD}}\)
Do đó:\(\frac{{QG}}{{GD}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GP}}{{GC}} = \frac{1}{3}\)
Suy ra điều cần chứng minh.
CM
20 tháng 4 2019
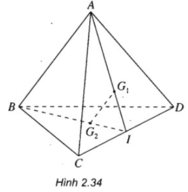
Gọi I là trung điểm của CD.
Vì G 1 là trọng tâm của tam giác ACD nên G 1 ∈ A I
Vì G 2 là trọng tâm của tam giác BCD nên G 2 ∈ B I
Ta có :
A B ⊂ ( A B C ) ⇒ G 1 G 2 / / ( A B C )
Và A B ⊂ ( A B D ) ⇒ G 1 G 2 / / ( A B D )
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
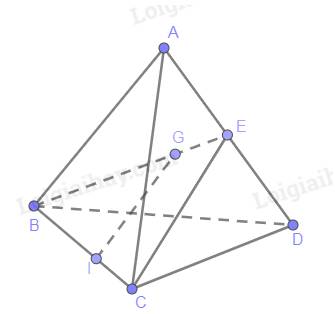
Tam giác BCE có E là trung điểm AD
Suy ra:\(\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}\)
Theo Ta lét, IG //CE
Mà CE thuộc (ACD)
Suy ra: IG // (ACD)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
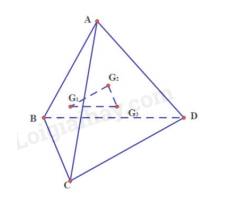
a) Gọi E, F, H là trung điểm của BC, CD, BD
Ta có:\({G_1}\) là trọng tâm tam giác ABC, suy ra\(\frac{{A{G_1}}}{{AE}} = \frac{2}{3}\)
\({G_3}\)là trọng tâm tam giác ABD, suy ra\(\frac{{A{G_3}}}{{AH}} = \frac{2}{3}\)
Suy ra tam giác AEH có\(\frac{{A{G_1}}}{{AE}} = \frac{{A{G_3}}}{{AH}}\) nên \({G_1}{G_3}//EH\)
Mà EH thuộc (BCD) nên \({G_1}{G_3}//(BCD)\)
Tương tự ta có:\({G_2}{G_3}//(BCD)\)
Do đó, \({G_1}{G_2}{G_3}//(BCD)\)
b) Ta có: \({G_1}{G_2}{G_3}//(BCD)\) nên \({G_1}{G_2} // BD\)
mà \({G_3}\) là điểm chung của hai mặt phẳng
Từ \({G_3}\) kẻ \({G_3}x\) sao cho \({G_3}x//BD\)
Vậy \({G_3}x\) là giao tuyến cần tìm.
a: Gọi giao điểm của AG với BC là E
Xét ΔABD có
G là trọng tâm
E là giao điểm của AG với BD
Do đó: E là trung điểm của BD và AG=2/3AE
Xét ΔAHD có \(\dfrac{AG}{AE}=\dfrac{AM}{AD}=\dfrac{2}{3}\)
nên GM//ED
=>GM//BD
mà BD\(\subset\left(BCD\right)\) và GM không thuộc mp(BCD)
nên GM//(BCD)
b: Gọi giao của AH với BC là F
Xét ΔABC có
H là trọng tâm
F là giao điểm của AH với BC
Do đó: F là trung điểm của BC và AH=2/3AF
Xét ΔAGE có \(\dfrac{AH}{AF}=\dfrac{AG}{AE}=\dfrac{2}{3}\)
nên HG//FE
mà \(FE\subset\left(BCD\right)\);HG không thuộc(BCD)
nên HG//(BCD)
Vẽ hình minh họa dc kh ạ