a) Cho x+y=1. tính A= \(x^3+y^3+3xy\)
b) Cho x-y=1 . Tính B= \(x^3-y^3-3xy\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) cho x+y=1. Tính giá trị biểu thức x^3+ y^3+ 3xy
b) cho x-y=1. Tính giá trị biểu thức x^3- y^3- 3xy

x^3+ y^3+ 3xy
=(x+y)(x^2 -xy + y^2 ) + 3xy
=x^2 -xy + y^2 + 3xy
=x^2 + 2xy + y^2
=(x+y)^2 =1
=> x^3+ y^3+ 3xy=1

a, \(x^3+y^3+3xy=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy=x^2-xy+y^2+3xy=x^2+2xy+y^2=\left(x+y\right)^2=1\)
b, tương tự a
c, Sửa đề Cho a+b=1. Tính giá trị của các biểu thứ :A= a3+b3+3ab(a2+b2)+ 6a2b2(a+b)
\(A=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab\left[\left(a+b\right)^2-2ab\right]+6a^2b^2\left(a+b\right)\)
\(=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]+3ab\left[\left(a+b\right)^2-2ab\right]+6a^2b^2\left(a+b\right)\)
Thay a+b=1 vào A ta có:
\(A=1-3ab+3ab\left(1-2ab\right)+6a^2b^2\)
\(=1-3ab+3ab-6a^2b^2+6a^2b^2=1\)
d. \(B=x^2+2xy+y^2-4x-4y+1=\left(x+y\right)^2-4\left(x+y\right)+1=\left(x+y\right)\left(x+y-4\right)+1\)
Thay x+y=3 vào B ta có:
\(B=3\left(3-4\right)+1=3.\left(-1\right)+1=-3+1=-2\)

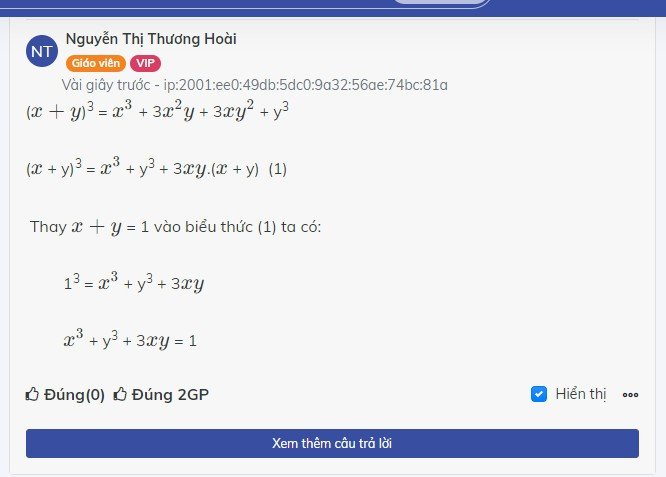
a) Vì x + y = 1 => ( x + y )3 = 1
=> x3 + 3x2y + 3xy2 + y3 = 1
=> x3 + y3 + 3xy ( x + y ) = 1
=> x3 + y3 +3xy = 1 (do x+y=1)
b) x-y=1 => (x-y)3=1
=> x3 - 3x2y + 3xy2 -y3 = 1
=> x3 -y3 - 3xy (x - y) = 1
=> x3 - y3 -3xy =1 (do x-y=1)

\(A=x^3+y^3+3xy=\left(x+y\right)^3-3xy\left(x+y\right)+3xy=1+0=1\)
\(B=\left(x-y\right)^3+3xy\left(x-y\right)-3xy=1\)
\(c,M=a^2-ab+b^2+3ab\left(a^2+b^2\right)+6a^2b^2=3ab\left(a^2+2ab+b^2\right)+a^2-ab+b^2\)
\(=3ab+a^2-ab+b^2=\left(a+b\right)^2=1\)
\(x+y=2;x^2+y^2=10\text{ do đó:}xy=-3\text{ nên }\left(x-y\right)^2=16\text{ do đó: }x-y=4\text{ hoặc }x-y=-4\)
\(\text{giải ra được:}x=3;y=-1\text{ hoặc ngược lại nên }x^3+y^3=-26\text{ hoặc }26\)
A = x3 + y3 + 3xy
= x3 + 3x2y + 3xy2 + y3 - 3x2y - 3xy2 + 3xy
= ( x3 + 3x2 + 3xy2 + y3 ) - ( 3x2y + 3xy - 3xy )
= ( x + y )3 - 3xy( x + y - 1 )
= 13 - 3xy( 1 - 1 )
= 13 - 3xy.0
= 1 - 0 = 1
Vậy A = 1
b) B = x3 - y3 - 3xy
= x3 - 3x2y + 3xy2 - y3 + 3x2y - 3xy2 - 3xy
= ( x3 - 3x2y + 3xy2 - y3 ) + ( 3x2y - 3xy2 - 3xy )
= ( x - y )3 + 3xy( x - y - 1 )
= 13 + 3xy( 1 - 1 )
= 1 + 3xy.0
= 1 + 0 = 1
Vậy B = 1
M = a3 + b3 + 3ab( a2 + b2 ) + 6a2b2( a + b )
= ( a + b )( a2 - ab + b2 ) + 3ab[ ( a + b )2 - 2ab ] + 6a2b2( a + b )
= ( a + b )[ ( a + b )2 - 3ab ] + 3ab[ ( a + b )2 - 2ab ] + 6a2b2( a + b )
= 1.( 1 - 3ab ) + 3ab( 1 - 2ab ) + 6a2b2.1
= 1 - 3ab + 3ab - 6a2b2 + 6a2b2
= 1
Vậy M = 1
d) x + y = 2
⇔ ( x + y )2 = 4
⇔ x2 + 2xy + y2 = 4
⇔ 10 + 2xy = 4 ( gt x2 + y2 = 10 )
⇔ 2xy = -6
⇔ xy = -3
x3 + y3 = x3 + 3x2y + 3xy2 + y3 - 3x2y - 3xy2
= ( x3 + 3x2y + 3xy2 + y3 ) - ( 3x2y + 3xy2 )
= ( x + y )3 - 3xy( x + y )
= 23 - 3.(-3).(2)
= 8 + 18 = 26

Các bài này đưa về dạng Hằng đẳng thức là được . Làm ra dài lắm bạn ạ !

b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)

A=x^3 + y^3 + 3xy(x+y)
=x+3x^y+3xy^2+y^3
=(x+y)^3=2^3=8
B=x^2+2xy+y^2+4
=(x+y)^2+4=4+4=8
C=x^3+y^3+3xy(x+y)+7(x+y)
=(x+y)^3+7(x+y)
=2^3+7.2
=8+14=22