Làm hết giúp mình luôn ạ cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{2}{x-2}+\dfrac{3}{x+2}+\dfrac{18-5x}{4-x^2}=\dfrac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4+3x-6+5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10x-20}{\left(x-2\right)\left(x+2\right)}=\dfrac{10\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10}{x+2}\)

mình làm những bài bn chưa lm nhé
9B
10A
bài 2
have repainted
bàii 3
ride - walikking
swimming
watch


Em tách ra 1-2 bài/1 câu hỏi để mọi người hỗ trợ nhanh nhất nha!


\(=\left(\dfrac{1}{49}-\dfrac{1}{9}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49^2}\right)=0\)

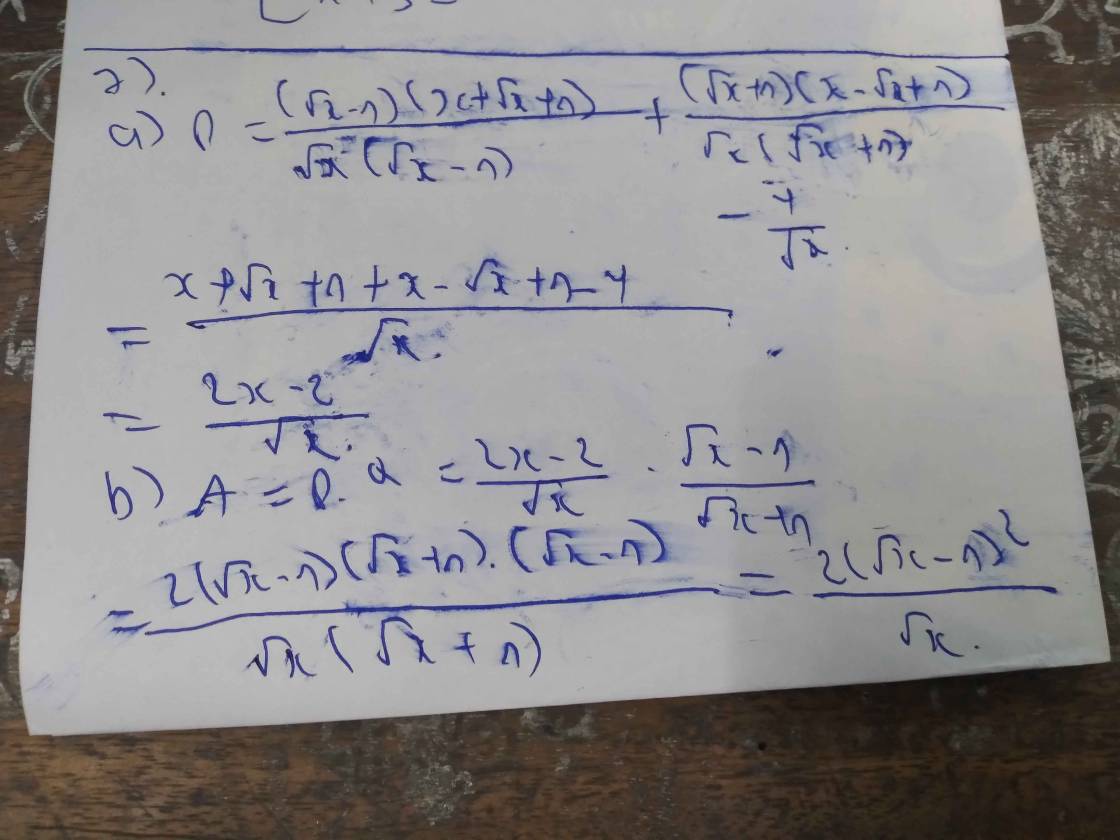

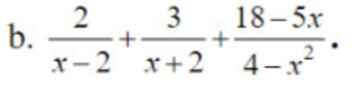 Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn
Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn




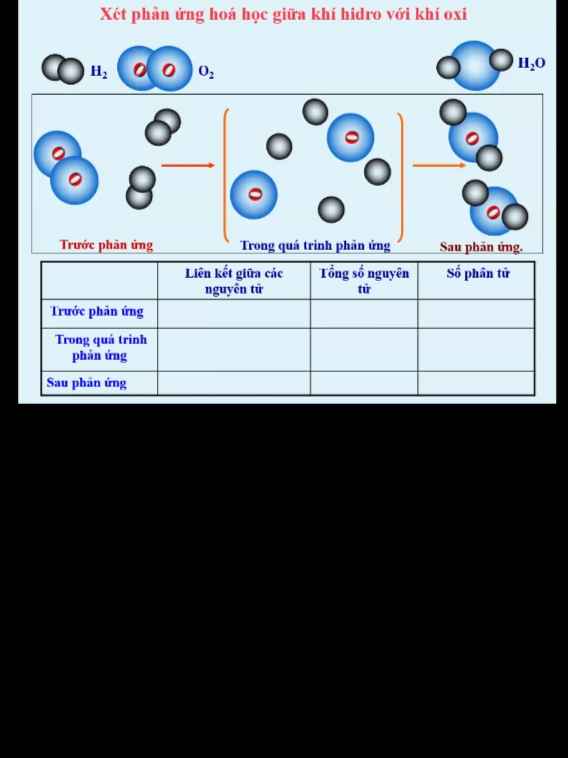


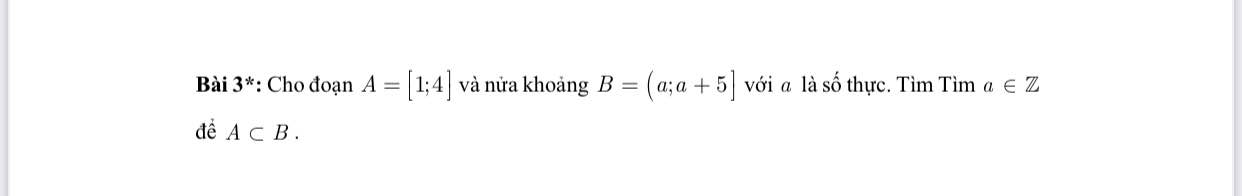
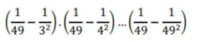
5:
a: Giả thiết: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba
Kết luận: Hai đường thẳng đó song song
b:
6:
a: \(\widehat{A_1}\) đồng vị với \(\widehat{B_4}\)
góc A4 là góc so le trong với góc B4
b: \(\widehat{A_2}=\widehat{A_3}\)(hai góc đối đỉnh)
mà \(\widehat{A_3}=140^0\)
nên \(\widehat{A_2}=140^0\)
\(\widehat{A_2}=\widehat{B_3}\)(đồng vị, a//b)
mà \(\widehat{A_2}=140^0\)
nên \(\widehat{B_3}=140^0\)
c: \(\widehat{A_4}=180^0-140^0=40^0\)
ΔBHA vuông tại H
=>\(\widehat{HBA}+\widehat{HAB}=90^0\)
=>\(\widehat{HBA}=90^0-40^0=50^0\)