Một con lắc lò xo khối lượng 400g, độ cứng 200Newton/m, kéo con lắc ra khỏi vị trí cân bằng 2cm rồi truyền cho nó 1 vận tốc 20 √ 2 cm/s theo chiều dương. Viết phương trình giao động, chọn gốc thời gian là lúc vật ở vị trí cân bằng .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án B
Cách 1: Giải truyền thống
Biên độ dao động: A = x 2 + v 2 ω 2 = x 2 + v 2 m k = 3 2 + 30 2 .1 100 = 3 2 c m
Khi t = 0 → x = 3 → A = 3 2 x = A 2 v < 0 ⇒ φ = π 4 ⇒ 3 2 cos 10 t + π 4 c m
Cách 2: Dùng máy tính cầm tay
Cơ sở lí thuyết: x = A cos ω t + φ → t = 0 x ¯ = A cos φ + i sin φ (Biểu diễn phức).
Mặt khác: t = 0 → x = A cos φ v = − A ω sin φ ⇒ x ¯ = A cos φ + i sin φ = x − v ω i .
Bước 1: Bấm S H I F T M o d e 4 (Cài chế độ rad).
Bước 2: M o d e 2 S H I F T M o d e ∨ 3 2 (Cài chế độ tính toán).
Nhập biểu thức 3 − − 30 10 i màn hình xuất hiện.
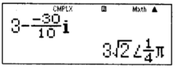
Chú ý: Do gốc tọa độ và chiều truyền vận tốc ta có x = 3 ; v < 0 . Các trường hợp khác thì dấu của x và v có thể thay đổi, bạn đọc cẩn thận chọn dấu cho phù hợp, tránh trường hợp chọn nhầm và nhập máy từ đó dẫn đến kết quả sai.

T = 0,63s ⇒ ω = 10
Tại t = 0 vật ở biên dương nên phương trình dao động của vật là
x = 10cos10t (cm)

Đáp án C
Phương pháp : Sử dụng lí thuyết về phương trình dao động điều hoà
Cách giải:
Tần số góc:
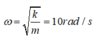
Khi x = 3 2 thì v = 0 nên
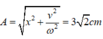
Chọn gốc thời gian t = 0 là lúc vật qua vị trí x = - 3cm theo chiều dương.
Biểu diễn trên đường tròn lượng giác ta được pha ban đầu φ = - 3 π 4
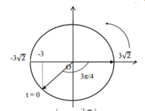
Phương trình dao động điều hòa: x = 3 2 cos 10 t - 3 π 4 cm
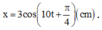
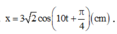
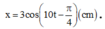
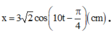

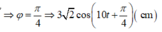

Chu kì dao động con lắc lò xo:
\(T=2\pi\cdot\sqrt{\dfrac{m}{k}}=2\pi\cdot\sqrt{\dfrac{0,4}{200}}=\dfrac{\pi\sqrt{5}}{25}\left(s\right)\)
Tần số góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{\pi\sqrt{5}}{25}}=10\sqrt{5}\left(rad\right)\)
Biên độ dao động:
\(A=\sqrt{x^2+\dfrac{v^2}{\omega^2}}=\sqrt{2^2+\dfrac{\left(20\sqrt{2}\right)^2}{\left(10\sqrt{5}\right)^2}}=\dfrac{2\sqrt{35}}{5}\approx2,4\left(cm\right)\)
Gốc thời gian là lúc vật ở VTCB nên \(\varphi_0=0\)
PT dao động:
\(x=Acos\left(\omega t+\varphi_0\right)=2,4cos\left(10\sqrt{5}t\right)\) (cm)