Cho 9 quả bóng được đánh số từ 1-9. có bao nhiêu cách lấy ra cùng lúc 2 quả bóng có tổng là số chẵn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong trường hợp xấu nhất ta chọn phải tất cả các quả số 1, 2, ..., 9
và mỗi số từ 10 đến 100 mỗi số có 9 quả. Như vậy có tất cả 45+ 9×91 = 864
quả. Vậy phải lấy ít nhất 865 quả để đảm bảo có 10 quả cùng số.
Đáp số: 865.

Số phần tử của không gian mẫu là ![]()
Các trường hợp thuận lợi cho biến cố là
• 2 xanh, 1 vàng, 1 đỏ ![]() (Giải thích: Khi bốc mình sẽ bốc bi ít hơn trước tiên. Bốc 2 viên bi xanh từ 4 viên bi xanh nên có
(Giải thích: Khi bốc mình sẽ bốc bi ít hơn trước tiên. Bốc 2 viên bi xanh từ 4 viên bi xanh nên có 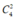 cách, tiếp theo bốc 1 viên bi vàng từ 3 viên bi vàng (do loại 2 viên cùng số với bi xanh đã bốc) nên có
cách, tiếp theo bốc 1 viên bi vàng từ 3 viên bi vàng (do loại 2 viên cùng số với bi xanh đã bốc) nên có ![]() cách, cuối cùng bốc 1 viên bi đỏ từ 3 viên bi đỏ (do loại 2 viên cùng số với bi xanh và 1 viên cùng số với bi vàng) nên có
cách, cuối cùng bốc 1 viên bi đỏ từ 3 viên bi đỏ (do loại 2 viên cùng số với bi xanh và 1 viên cùng số với bi vàng) nên có ![]() cách)
cách)
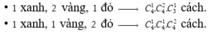
Suy ra số phần tử của biến cố là ![]()
Vậy xác suất cần tính 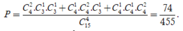
Chọn C.

Chọn đáp án C

Các trường hợp thuận lợi cho biến cố là
![]()
§ (Giải thích: Khi bốc mình sẽ bốc bi ít hơn trước tiên. Bốc 2 viên bi xanh từ 4 viên bi xanh nên có cách, tiếp theo bốc 1 viên bi vàng từ 3 viên bi vàng (do loại 2 viên cùng số với bi xanh đã bốc) nên có C 3 1 cách, cuối cùng bốc 1 viên bi đỏ từ 3 viên bi đỏ (do loại 2 viên cùng số với bi xanh và 1 viên cùng số với bi vàng) nên có C 3 1 cách).


Muốn lấy số bóng ít nhất mà chắc chắn được 4 quả cùng màu thì ít nhất phải lấy hết số bóng có 3 màu mà có số lượng ít nhất và lấy thêm 1 quả nữa.
Vậy số bóng ít nhất Moris cần lấy ra l
2+3+9+1 = 15 (qu
ả)à:quả)

Đáp án C
Phương pháp:
Chia thành các trường hợp:
+ Trong hai quả bóng bốc được có ít nhất một quả có số chia hết cho 10.
+ Trong hai quả bốc được có một quả có chữ số hàng đơn vị bằng 5 và một quả có chữ số hàng đơn vị là 2,4,6,8.
Đếm số khả năng có lợi cho biến cố và tính xác suất.
Cách giải:
Xét phép thử T: “Bốc ngẫu nhiên 2 trong 50 quả bóng”.
Số phần tử không gian mẫu n Ω = C 50 2
Gọi A là biến cố: “Tích hai số ghi trên hai bóng chia hết cho 10:.
+) TH1: Trong hai quả bốc được có ít nhất 1 quả có số chia hết cho 10
Số cách chọn để trong hai quả không có quả nào có số chia hết cho 10 là C 45 2
→ Số cách chọn để trong hai quả có ít nhất 1 quả có số chia hết cho 10 là
![]()
+) TH2: Trong hai quả bốc được có 1 quả có chữ số hàng đơn vị là 5 và 1 quả có chữ số hàng đơn vị là 2,4,6,8.
Số cách chọn để có được hai số trên (không phân biệt thứ tự) là
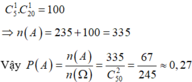

Chọn C
![]() .
.
Gọi là biến cố “bốc được quả bóng có tích của số ghi trên quả bóng là một số chia hết cho 10 ”. Xét các tập hợp sau:
![]()
 Tập
B
2
có 20 phần tử.
Tập
B
2
có 20 phần tử.
![]()
Có ba trường hợp xảy ra khi tích của hai số trên hai quả bóng chia hết cho 10.
Trường hợp 1: 1 quả bóng có số ghi thuộc tập B 1 , quả bóng còn lại có số ghi thuộc tập B\ B 1
Khi đó số cách bốc 2 quả bóng là: ![]() (cách).
(cách).
Trường hợp 2: 2 quả bóng có số ghi đều thuộc tập B 1 .
Khi đó số cách bốc 2 quả bóng là: C 5 2 (cách).
Trường hợp 3: 1 quả bóng có số ghi thuộc tập B 2 , quả bóng còn lại có số ghi thuộc tập C 2 .
Khi đó số cách bốc 2 quả bóng là: ![]()
Suy ra: ![]()
Vậy:
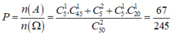
=> 0,25 < P < 0,3


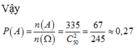

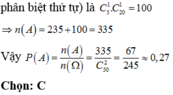
Trong 9 quả bóng sẽ có 5 quả bóng được đánh số lẻ và 4 quả bóng được đánh số chẵn
TH1: 2 quả đều lẻ
=>Có \(C^2_5=10\left(cách\right)\)
TH2: 2 quả đều chẵn
=>Có \(C^2_4=6\left(cách\right)\)
Số cách lấy ra cùng lúc 2 quả bóng có tổng là số chẵn là:
10+6=16(cách)