cho tam giác vuông tại A,trung tuyến AM.Kẻ MD vuông góc AB(D thuộc AB),MEvuoong góc AC(E thuộc AC) .
a) tứ giác ADME là hình gì?Vì sao?
b) kẻ dường cao AH của tam giác ABC, trên tia đối của tia HA lấy điểm I sao cho HI=HA trên tia đối của tia HB lấy điểm K sao cho HK=HB.chứng minh AK vuông góc IC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

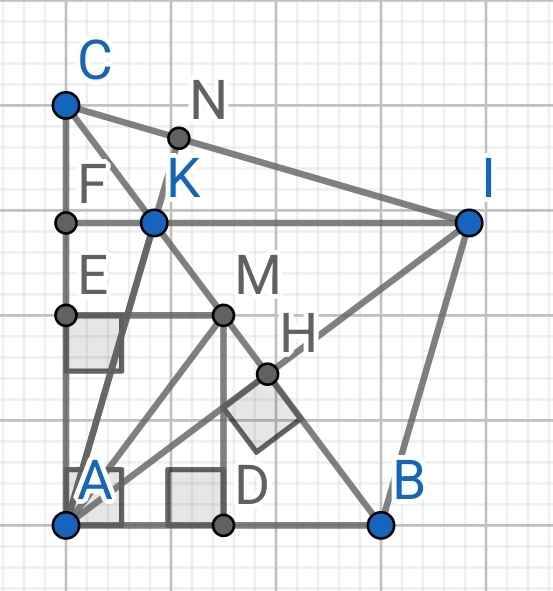
a) Tứ giác ADME có:
∠AEM = ∠ADM = ∠EAD = 90⁰ (gt)
⇒ ADME là hình chữ nhật
b) Do HI = HA (gt)
⇒ H là trung điểm của AI
Do HK = HB (gt)
⇒ H là trung điểm của BK
Tứ giác ABIK có:
H là trung điểm của AI (cmt)
H là trung điểm của BK (cmt)
⇒ ABIK là hình bình hành
⇒ IK // AB
Mà AB ⊥ AC (∆ABC vuông tại A)
⇒ IK ⊥ AC
⇒ IK là đường cao của ∆ACI
Lại có:
AH ⊥ BC (do AH là đường cao của ∆ABC)
⇒ CH ⊥ AI
⇒ CH là đường cao thứ hai của ∆ACI
∆ACI có:
IK là đường cao (cmt)
CH là đường cao (cmt)
⇒ AK là đường cao thứ ba của ∆ACI
⇒ AK ⊥ IC

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
Do đó: ADME là hình chữ nhật
b: I,K ở đâu vậy bạn?

a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
Do đó: AEMF là hình chữ nhật
b: Xét tứ giác ABDK có
H là trung điểm chung của AD và BK
=>ABDK là hình bình hành
Hình bình hành ABDK có AD\(\perp\)BK
nên ABDK là hình thoi

a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
=>ADME là hình chữ nhật
b: ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
c: Xét ΔBMP có
BD vừa là đường cao, vừa là đường trung tuyến
Do đó: ΔBMP cân tại B
=>BA là phân giác của góc MBP
Xét ΔAMP có
AD là đường cao, là đường trung tuyến
Do đó: ΔAMP cân tại A
=>AB là phân giác của góc MAP(1)
Xét ΔAMQ có
AC vừa là đường cao, vừa là đường trung tuyến
Do đó; ΔAMQ cân tại A
=>AC là phân giác của góc MAQ(2)
Từ (1), (2) suy ra góc PAQ=2*góc BAC=180 độ
=>P,A,Q thẳng hàng
Xét ΔAMB và ΔAPB có
AM=AP
AB chung
BM=BP
Do đó: ΔAMB=ΔAPB
=>góc AMB=góc APB
Xét ΔAMC và ΔAQC có
AM=AQ
góc MAC=góc QAC
AC chung
Do đó: ΔAMC=ΔAQC
=>góc AMC=góc AQC
=>góc AQC+góc AMB=180 độ
mà góc AMB=góc APB
nên góc AQC+góc APB=180 độ
=>BP//QC
=>BPQC là hình thang
d: AM=AP
AM=AQ
Do đó: AP=AQ
mà P,A,Q thẳng hàng
nên A là trung điểm của PQ

a: Xét tứ giác ANDM có
\(\widehat{AND}=\widehat{AMD}=\widehat{MAN}=90^0\)
=>ANDM là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của CB
DN//AB
Do đó: N là trung điểm của AC
Xét tứ giác ADCEcó
N là trung điểm chung của AC và DE
=>ADCE là hình bình hành
Hình bình hành ADCE có AC\(\perp\)DE
nên ADCE là hình thoi
c:
Xét ΔABC có
D là trung điểm của BC
DM//AC
Do đó: M là trung điểm của AB
Để AMDN là hình vuông thì AM=AN
mà \(AM=\dfrac{AB}{2};AN=\dfrac{AC}{2}\)
nên AB=AC

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
b: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
nên ADME là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó E là trung điểm của AC
Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
=>ME//BD và ME=BD
=>MEDB là hình bình hành
=>MD cắtEB tại trung điểm của mỗi đường
=>B,K,E thẳng hàng

a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
Do đó: ADME là hình chữ nhật
b:ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
c: Xét ΔAMQ có
AE vừa là đường cao, vừa là trung tuyến
=>ΔAMQ cân tại A
=>AE là phân giác của góc MAQ(1)
Xét ΔAMP có
AD vừa là đường cao, vừa là trung tuyến
=>ΔAMP cân tại A
=>AD là phân giác của góc MAP(2)
Từ (1), (2) suy ra góc PAQ=góc MAP+góc MAQ
=2(góc BAM+góc CAM)
=2*góc BAC
=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ=AM
nên A là trung điểm của PQ

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b: Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot4\cdot6=2\cdot6=12\left(cm^2\right)\)
Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
=>\(AD=DB=\dfrac{AB}{2}=2\left(cm\right)\)
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
=>\(AE=EC=\dfrac{AC}{2}=3\left(cm\right)\)
Diện tích hình chữ nhật ADME là:
\(S_{ADME}=AD\cdot AE=2\cdot3=6\left(cm^2\right)\)
c: Để hình chữ nhật ADME trở thành hình vuông thì AD=AE
mà AD=AB/2; AE=AC/2
nên AB=AC
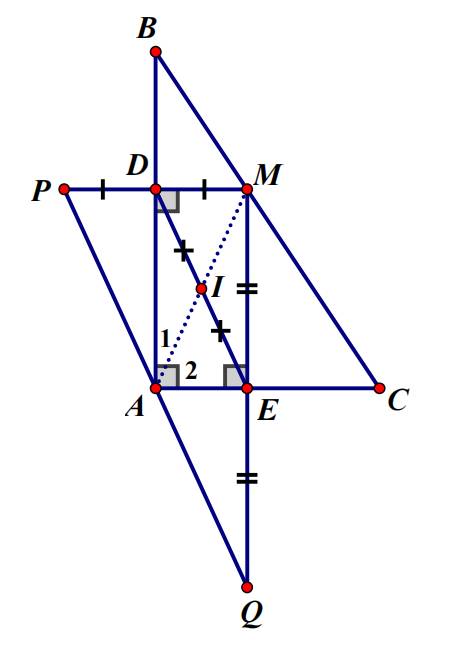
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b: Xét tứ giác ABKI có
M là trung điểm chung của AK và BI
Do đó: ABKI là hình bình hành
=>KI//AB
mà AB\(\perp\)AC
nên KI\(\perp\)AC
Xét ΔCAI có
IK,CH là đường cao
IK cắt CH tại K
Do đó: K là trực tâm của ΔCAI
=>AK\(\perp\)IC