cho tam giác ABC vuông tại A có AC=20cm.Kẻ AH vuông góc với BC.Biết BH=9cm,HC=16cm.Tính độ các cạnh góc vuông AB và AC
help meee
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
21 tháng 10 2023
Đúng(2)
Những câu hỏi liên quan
14 tháng 5 2022
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
\(AB=\sqrt{9^2+12^2}=15\left(cm\right)\)
14 tháng 5 2022
\(BC=BH+HC=9+16=25\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=15\left(cm\right)\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=BH^2+AH^2\)
\(\rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=12\left(cm\right)\)
10 tháng 11 2023
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=50^2-30^2=1600\)
=>AC=40(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=HB\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(BH=\dfrac{30^2}{50}=18\left(cm\right);CH=\dfrac{40^2}{50}=32\left(cm\right)\)
TP
10 tháng 11 2023
Áp dụng định lý Pytago vào \(\Delta ABC\) vuông tại A ta có:
\(AB^2+AC^2=BC^2\Rightarrow AC^2=BC^2-AB^2=50^2-30^2=1600\Rightarrow AC=\sqrt{1600}=40\left(cm\right)\)
Áp dụng định lý Pytago vào \(\Delta ABH\) vuông tại H ta có: \(AH^2+BH^2=AB^2\Rightarrow24^2+BH^2=30^2\Rightarrow BH^2=30^2-24^2=324\Rightarrow BH=\sqrt{324}=18\left(cm\right)\)\(HC=BC-BH=50-18=32\left(cm\right)\)
TD
1
23 tháng 1 2017
Bạn đã hk định lí Pi-ta-go chưa ? Nếu hk rồi thì sau đây là cách giải:
tam giác ABH vuông tại H. Áp dụng định lí Pi-ta-go ta có:
AH2=AB2-BH2=52-32=16 => AH=4
Ta có: HC=BC-BH=8-3=5 =>HC=5
Tam giác AHC vuông tại H. Áp dụng định lí Pi-ta-go ta có:
AC2=AH2+HC2=42+52=41
Nếu có sai ở đâu thì sửa đi nhé !
14 tháng 7 2023
Bài 3 :
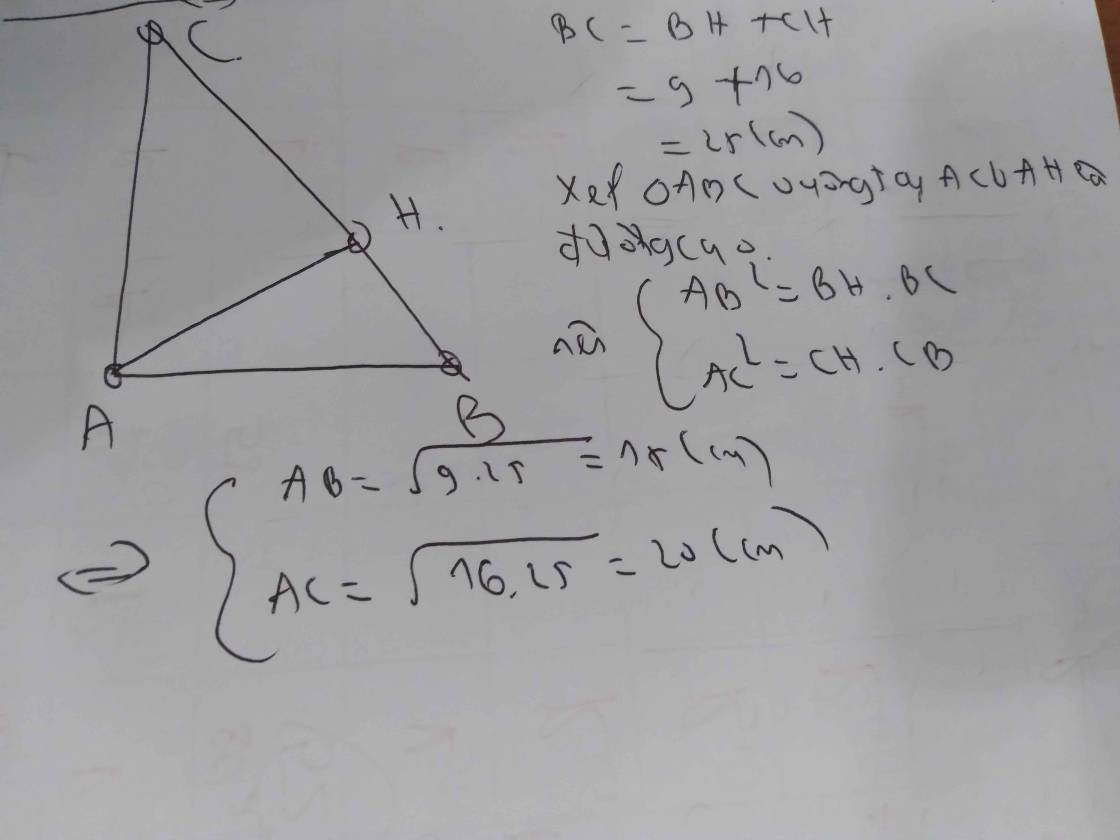
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)
14 tháng 6 2017
Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm