Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

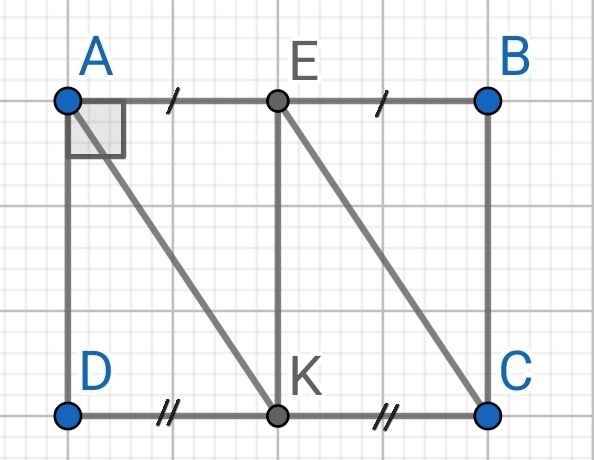 a) Do E là trung điểm của AB (gt)
a) Do E là trung điểm của AB (gt)
⇒ AE = AB : 2
Do K là trung điểm của CD (gt)
⇒ CK = DK = CD : 2
Mà AB = CD (do ABCD là hình chữ nhật)
⇒ AE = CK
Lại có AB // CD (do ABCD là hình chữ nhật)
⇒ AE // CK
Tứ giác AECK có:
AE // CK (cmt)
AE = CK (cmt)
⇒ AECK là hình bình hành
b) Do AE = AB : 2 (cmt)
DK = CD : 2 (cmt)
AB = CD (cmt)
⇒ AE = DK
Lại có:
AB // CD (cmt)
⇒ AE // DK
Tứ giác AEKD có:
AE // DK (cmt)
AE = DK (cmt)
⇒ AEKD là hình bình hành
Mà ∠EAK = 90⁰ (do ABCD là hình chữ nhật)
⇒ AEKD là hình chữ nhật
⇒ ∠AEK = 90⁰
Hay AE ⊥ EK

a)ta có:
AB=DC mà AE=1/2 AB, KC= 1/2 DC
=>AE=KC
Xét tứ giác AECK, ta có:
AE//KC(AB//KC và AE thuộc AB và KC thuộc DC)
=>tứ giác AECK là hình bình hành.
b) chỗ DE vuông góc CE có đúng không vậy để mai mình làm tiếp

a: Xét tứ giác AECK có
AK//CE
AK=CE
Do đó: AECK là hình bình hành

1: E là trung điểm của AB
=>\(EA=EB=\dfrac{AB}{2}\)(1)
K là trung điểm của CD
=>\(DK=KC=\dfrac{DC}{2}\)(2)
ABCD là hình vuông
=>AB=DC(3)
Từ (1),(2),(3) suy ra AE=EB=CK=KD
Xét tứ giác AECK có
AE//CK
AE=CK
Do đó: AECK là hình bình hành
2: Xét ΔFCD vuông tại C và ΔEBC vuông tại B có
FC=EB
CD=BC
Do đó: ΔFCD=ΔEBC
=>\(\widehat{FDC}=\widehat{ECB}\)
mà \(\widehat{FDC}+\widehat{DFC}=90^0\)(ΔDFC vuông tại C)
nên \(\widehat{ECB}+\widehat{DFC}=90^0\)
=>DF\(\perp\)CE tại M
3: AECK là hình bình hành
=>AK//CE
AK//CE
CE\(\perp\)DF
Do đó: AK\(\perp\)CE tại N
Xét ΔDMC có
K là trung điểm của DC
KN//MC
Do đó: N là trung điểm của DM
4: Xét ΔADM có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔADM cân tại A
=>AD=AM
mà AD=AB
nên AM=AB

Ta có
góc FAD+DAE=90•
DAE+EAB=90•
-> FAD=EAB
xet tam giác AEB và tam giác ADF có
AB=AD( ABCD là hình vuông)
ABE=ADF=90•
FAD=EAB
suy ra tam giac ABE=tam giác ADF(g.c.g)
-> AF=AE

a: Xét tứ giác AECK có
AK//CE
AK=CE
=>AECK là hình bình hành
b: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm của AC
AECK là hbh
=>AC cắt EK tại trung điểm của mỗi đường
=>E,O,K thẳng hàng
c: Xét ΔDMC có
E là trung điểm của DC
EN//MC
=>N là trung điểm của DM
=>DN=NM
Xét ΔABN có
K là trung điểm của BA
KM//AN
=>M là trung điểm của BN
=>MB=MN=DN
⇒ AE = AB : 2
Do K là trung điểm của CD (gt)
⇒ CK = DK = CD : 2
Mà AB = CD (do ABCD là hình chữ nhật)
⇒ AE = CK
Lại có AB // CD (do ABCD là hình chữ nhật)
⇒ AE // CK
Tứ giác AECK có:
AE // CK (cmt)
AE = CK (cmt)
⇒ AECK là hình bình hành
b) Do AE = AB : 2 (cmt)
DK = CD : 2 (cmt)
AB = CD (cmt)
⇒ AE = DK
Lại có:
AB // CD (cmt)
⇒ AE // DK
Tứ giác AEKD có:
AE // DK (cmt)
AE = DK (cmt)
⇒ AEKD là hình bình hành
Mà ∠EAK = 90⁰ (do ABCD là hình chữ nhật)
⇒ AEKD là hình chữ nhật
⇒ ∠AEK = 90⁰
Hay AE ⊥ EK