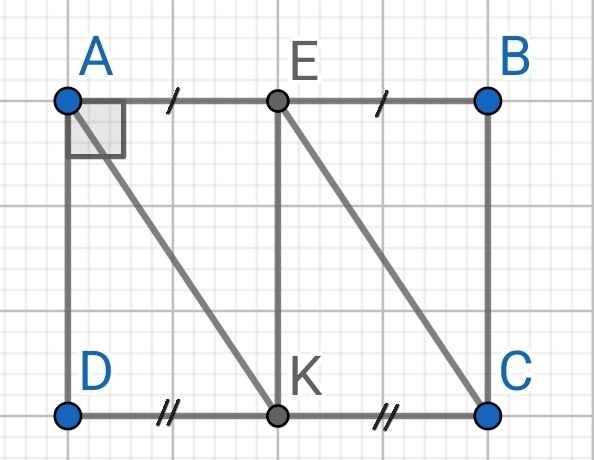
CHo HCN ABCD. Gọi E,K là trung điểm AB và CD
a/ c/minh Tgiác AECK là HBH
b/ c/minh AE vuông góc với EK
GIúp em với ạ! EM cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 a) Do E là trung điểm của AB (gt)
a) Do E là trung điểm của AB (gt)
⇒ AE = AB : 2
Do K là trung điểm của CD (gt)
⇒ CK = DK = CD : 2
Mà AB = CD (do ABCD là hình chữ nhật)
⇒ AE = CK
Lại có AB // CD (do ABCD là hình chữ nhật)
⇒ AE // CK
Tứ giác AECK có:
AE // CK (cmt)
AE = CK (cmt)
⇒ AECK là hình bình hành
b) Do AE = AB : 2 (cmt)
DK = CD : 2 (cmt)
AB = CD (cmt)
⇒ AE = DK
Lại có:
AB // CD (cmt)
⇒ AE // DK
Tứ giác AEKD có:
AE // DK (cmt)
AE = DK (cmt)
⇒ AEKD là hình bình hành
Mà ∠EAK = 90⁰ (do ABCD là hình chữ nhật)
⇒ AEKD là hình chữ nhật
⇒ ∠AEK = 90⁰
Hay AE ⊥ EK

a)ta có:
AB=DC mà AE=1/2 AB, KC= 1/2 DC
=>AE=KC
Xét tứ giác AECK, ta có:
AE//KC(AB//KC và AE thuộc AB và KC thuộc DC)
=>tứ giác AECK là hình bình hành.
b) chỗ DE vuông góc CE có đúng không vậy để mai mình làm tiếp

1: E là trung điểm của AB
=>\(EA=EB=\dfrac{AB}{2}\)(1)
K là trung điểm của CD
=>\(DK=KC=\dfrac{DC}{2}\)(2)
ABCD là hình vuông
=>AB=DC(3)
Từ (1),(2),(3) suy ra AE=EB=CK=KD
Xét tứ giác AECK có
AE//CK
AE=CK
Do đó: AECK là hình bình hành
2: Xét ΔFCD vuông tại C và ΔEBC vuông tại B có
FC=EB
CD=BC
Do đó: ΔFCD=ΔEBC
=>\(\widehat{FDC}=\widehat{ECB}\)
mà \(\widehat{FDC}+\widehat{DFC}=90^0\)(ΔDFC vuông tại C)
nên \(\widehat{ECB}+\widehat{DFC}=90^0\)
=>DF\(\perp\)CE tại M
3: AECK là hình bình hành
=>AK//CE
AK//CE
CE\(\perp\)DF
Do đó: AK\(\perp\)CE tại N
Xét ΔDMC có
K là trung điểm của DC
KN//MC
Do đó: N là trung điểm của DM
4: Xét ΔADM có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔADM cân tại A
=>AD=AM
mà AD=AB
nên AM=AB

Sửa đề: F là hình chiếu của E trên AC
a: Xét ΔCAB có
E là trung điểm của CB
EF//AB
=>F là trung điểm của AC
Xét ΔCAB có
E là trung điểm của CB
ED//AC
=>D là trung điểm của AB
Xét ΔABC có EF//AB
nên EF/Ab=CE/CB=1/2
=>EF=1/2AB=DB
Xét tứ giác BDFE có
FE//BD
FE=BD
=>BDFE là hình bình hành
b: Xét ΔABC có AD/AB=AF/AC
nên DF//BC
=>DF//EH
ΔHAC vuông tại H có HF là trung tuyến
nên HF=AC/2
=>HF=ED
Xét tứ giác EHDF có
EH//DF
ED=HF
=>EHDF là hình thang cân
c: Xét tứ giác ABCN có
F là trung điểm chung của AC và BN
=>ABCN là hình bình hành
=>AN//CB
Xét tứ giác AMCE có
F là trung điểm chung của AC và ME
=>AMCE là hình bình hành
=>AM//CE
=>AM//CB
mà AN//CB
nên A,N,M thẳng hàng
⇒ AE = AB : 2
Do K là trung điểm của CD (gt)
⇒ CK = DK = CD : 2
Mà AB = CD (do ABCD là hình chữ nhật)
⇒ AE = CK
Lại có AB // CD (do ABCD là hình chữ nhật)
⇒ AE // CK
Tứ giác AECK có:
AE // CK (cmt)
AE = CK (cmt)
⇒ AECK là hình bình hành
b) Do AE = AB : 2 (cmt)
DK = CD : 2 (cmt)
AB = CD (cmt)
⇒ AE = DK
Lại có:
AB // CD (cmt)
⇒ AE // DK
Tứ giác AEKD có:
AE // DK (cmt)
AE = DK (cmt)
⇒ AEKD là hình bình hành
Mà ∠EAK = 90⁰ (do ABCD là hình chữ nhật)
⇒ AEKD là hình chữ nhật
⇒ ∠AEK = 90⁰
Hay AE ⊥ EK