Chung to E=21+22+23+24+...+299 chia het cho 7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
PT
1
CM
19 tháng 4 2018
Ta có
2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100
= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )
= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2
= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98
Mà 7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7
Nên 2 + 7 2 2 + 2 5 + . . . + 2 98 : 7 d ư 2
PT
1
NB
1
27 tháng 12 2021
a,A=(2+22)+(23+24)+...+(22009+22010)
A=(1+2)(2+23+...+22009)=3(2+...+22009)⋮3
A=(2+22+23)+...+(22008+22009+22010)
A=(1+2+22)(2+...+22008)=7(2+...+22008)⋮7
27 tháng 2 2018
Tổng B có số số hạng là (299-21)/1+1=279( số hạng)
Giá trị của tổng B là \(\frac{\left(299+21\right).279}{2}=44640\)
Vì 44640\(⋮\)3 nên B\(⋮\)3 (đpcm)
NL
2
24 tháng 8 2021
`A=2^{0}+2^{1}+2^{2}+....+2^{99}`
`=(1+2+2^{2}+2^{3}+2^{4})+(2^{5}+2^{6}+2^{7}+2^{8}+2^{9})+......+(2^{95}+2^{96}+2^{97}+2^{97}+2^{99})`
`=(1+2+2^{2}+2^{3}+2^{4})+2^{5}(1+2+2^{2}+2^{3}+2^{4})+.....+2^{95}(1+2+2^{2}+2^{3}+2^{4})`
`=31+2^{5}.31+....+2^{95}.31`
`=31(1+2^{5}+....+2^{95})\vdots 31`
24 tháng 8 2021
\(A=2^0+2^1+2^2+2^3+2^4+2^5+2^6+...+2^{99}\)
\(=\left(2^0+2^1+2^2+2^3+2^4\right)+2^5\left(2^0+2^1+2^2+2^3+2^4\right)+...+2^{95}\left(2^0+2^1+2^2+2^3+2^4\right)=31+31.2^5+...+31.2^{95}=31\left(1+2^5+...+2^{95}\right)⋮31\)
NL
4
SS
24 tháng 8 2021
A = 20 + 21 + 22 + 23 + 24 + 25 … + 299
A=( 20 + 21 + 22 + 23 + 24) +( 25 … + 299)
A= 20.(20 + 21 + 22 + 23 + 24)+25.( 25 … + 299)
A= 1. 31+ 25.31… + 295.31
A= 31. (1+25...+295)
KL: ......
24 tháng 8 2021
\(A=2^0+2^1+2^2+2^3+2^4+...+2^{99}=\left(2^0+2^1+2^2+2^3+2^4\right)+2^5\left(2^0+2^1+2^2+2^3+2^4\right)+...+2^{95}\left(2^0+2^1+2^2+2^3+2^4\right)=31+31.2^5+...+31.2^{95}=31\left(1+2^5+...+2^{95}\right)⋮31\)
F
1
7 tháng 1 2021
Ta có: \(A=2+2^2+2^3+2^4+...+2^{99}+91\)
\(=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{97}+2^{98}+2^{99}\right)+91\)
\(=2\cdot\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{97}\left(1+2+2^2\right)+91\)
\(=7\cdot\left(1+2^4+...+2^{97}\right)+7\cdot13\)
\(=7\cdot\left(1+2^4+...+2^{97}+13\right)⋮7\)(đpcm)
PT
1
7 tháng 1 2021
Ta có: \(A=2+2^2+2^3+2^4+...+2^{99}\)
\(=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{97}+2^{98}+2^{99}\right)\)
\(=2\cdot\left(1+2+2^2\right)+2^4\cdot\left(1+2+2^2\right)+...+2^{97}\left(1+2+2^2\right)\)
\(=\left(1+2+2^2\right)\cdot\left(2+2^4+...+2^{97}\right)\)
\(=7\cdot\left(2+2^4+...+2^{97}\right)⋮7\)(đpcm)
DP
1
9 tháng 1 2023
A=(1+2+2^2)+2^3(1+2+2^2)+...+2^96(1+2+2^2)+2^99
=7(1+2^3+...+2^96)+2^99 ko chia hết cho 7
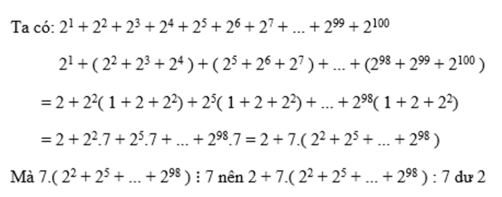
Ta có:\(7=2^0+2^1+2^2\)
Số số hạng của tổng E là: (99-1):1+1=99(số hạng)
Vì 99:3=33 nên ta có:
\(E=\left(2^1+2^2+2^3\right)+\left(2^4+2^5+2^6\right)\)\(+...+\left(2^{97}+2^{98}+2^{99}\right)\)
\(E=2.\)\(\left(2^0+2^1+2^2\right)\)\(+2^4.\left(2^0+2^1+2^2\right)+...+\)\(2^{97}.\left(2^0+2^2+2^2\right)\)
\(E=2.7+2^4.7+...+2^{97}.7\)
\(E=\left(2+2^4+...+2^{97}\right).7\)
Vì 7 chia hết cho 7 và \(2+2^4+...+2^{97}\)là số nguyên nên E chia hết cho 7
Vậy E chia hết cho 7
Bài mình có sai sót thì mọi người thông cảm và đóng góp ý kiến cho mình nha.