Bài 4. (1 điểm) Tại một hồ trong công viên nước, một con cá heo nhảy lên khỏi mặt nước với vận tốc ban đầu của cú nhảy là $20$ ft/giây, trong đó $1$ ft $=30,48$ cm.
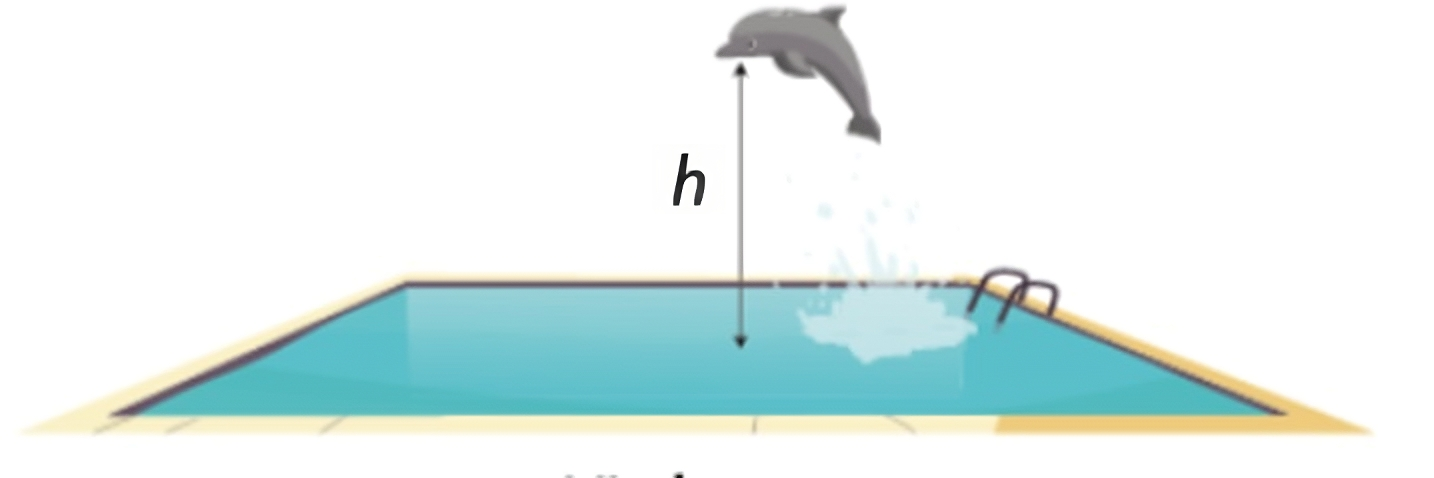
Độ cao $h$ (ft) của cá heo so với mặt nước sau thời gian $t$ giây kể từ lúc nhảy được tính bởi công thức $h=20 t-16 t^2$.
a) Phân tích công thức tính $h$ trên thành dạng tích của các đa thức.
b) Tính độ cao (cm) của cá heo so với mặt nước sau $0,5$ giây kể từ lúc nhảy. Làm tròn kết quả tới hàng đơn vị.

a) Số nhiệt của thành phố A là:
\(I=-45+2\cdot40+10\cdot100-0,2\cdot40\cdot100-0,007\cdot40^2-0,05\cdot100^2+0,001\cdot40^2\cdot100+0,009\cdot40\cdot100^2-0,000002\cdot40^2\cdot100^2\)
\(I=-3345,2\)
b) Số nhiệt của thành phố B là:
\(I=-45+2\cdot50+10\cdot90-0,007\cdot50^2-0,05\cdot90^2+0,001\cdot50^2\cdot90+0,009\cdot50\cdot90^2-0,00000\cdot50^2\cdot90^2\)
\(I=-3780\)
a) Số nhiệt của thành phố A là:
�=−45+2⋅40+10⋅100−0,2⋅40⋅100−0,007⋅402−0,05⋅1002+0,001⋅402⋅100+0,009⋅40⋅1002−0,000002⋅402⋅1002I=−45+2⋅40+10⋅100−0,2⋅40⋅100−0,007⋅402−0,05⋅1002+0,001⋅402⋅100+0,009⋅40⋅1002−0,000002⋅402⋅1002
�=−3345,2I=−3345,2
b) Số nhiệt của thành phố B là:
�=−45+2⋅50+10⋅90−0,007⋅502−0,05⋅902+0,001⋅502⋅90+0,009⋅50⋅902−0,00000⋅502⋅902I=−45+2⋅50+10⋅90−0,007⋅502−0,05⋅902+0,001⋅502⋅90+0,009⋅50⋅902−0,00000⋅502⋅902
�=−3780I=−3780