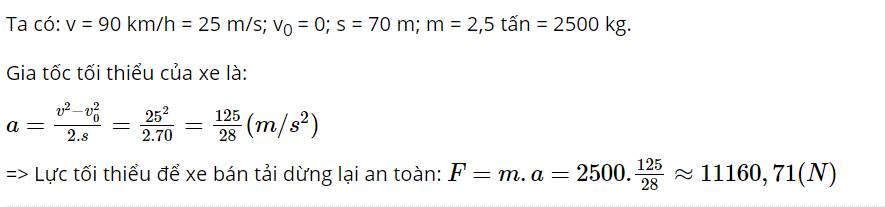Tính khoảng cách an toàn khi xe chạy với tốc độ 68km/h.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
23 tháng 2 2023
Trên đường cao tốc thường có các biển báo khoảng cách giúp lái xe có thể ước lượng khoảng cách giữa các xe để giữ khoảng cách an toàn khi tham gia giao thông.
QT
Quoc Tran Anh Le
Giáo viên
11 tháng 12 2023
Ta có: v = 90 km/h = 25 m/s; v0 = 0; s = 70 m; m = 2,5 tấn = 2500 kg.
Gia tốc tối thiểu của xe là:
\(a = \frac{{{v^2} - v_0^2}}{{2.s}} = \frac{{{{25}^2}}}{{2.70}} = \frac{{125}}{{28}}(m/{s^2})\)
=> Lực tối thiểu để xe bán tải dừng lại an toàn: \(F = m.a = 2500.\frac{{125}}{{28}} \approx 11160,71(N)\)
27 tháng 3 2022
Gọi S là quãng đường ô tô đi đến chỗ bạn An.
\(S_1\) là khoảng cách từ nơi bạn An đứng đến nơi ô tô đang đứng.
\(S_2\) là khoảng cách từ chỗ bạn An đến đường quốc lộ.
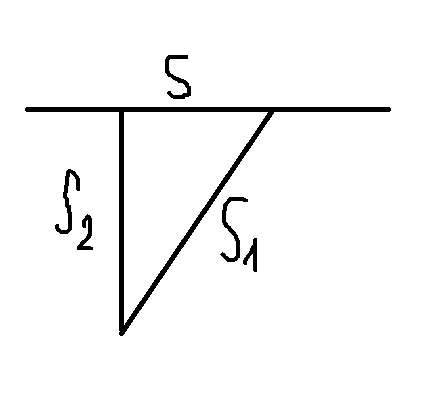
\(\Rightarrow S=\sqrt{S_1^2-S_2^2}=\sqrt{100^2-50^2}=50\sqrt{3}m\)
\(v=36\)km/h=10m/s
Thời gian ô tô đi đến chỗ bạn An:
\(t=\dfrac{S}{v}=\dfrac{50\sqrt{3}}{10}=5\sqrt{3}s\)
Vận tốc trung bình của An để vừa đón kịp xe:
\(v=\dfrac{S_1}{t}=\dfrac{100}{5\sqrt{3}}=\dfrac{20\sqrt{3}}{3}\approx11,55\)m/s
CM
20 tháng 6 2018
Đáp án A
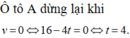
Quãng đường ô tô A đi được kể từ thời điểm bắt đầu hãm phanh đến lúc dừng lại là:
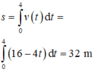
Do đó ô tô A phải hãm phanh khi cách ô tô B một khoảng tối thiểu là 32+1=33m
CM
19 tháng 7 2018
Đáp án A
Phương pháp
S = ∫ t 1 t 2 v t d t
Cách giải
v = 0 ⇒ t = 4
Quãng đường ô tô A đi được từ khi bắt đầu hãm phanh đến khi dừng hẳn
là S = ∫ 0 4 16 − 4 t d t = 32
Khi dừng lại ô tô A phải cách ô tô B tối thiểu 1m nên để có 2 ô tô A và B đạt khoảng cách an toàn thì ô tô A phải hãm phanh cách ô tô B một khoảng ít nhất là 33m.
TC
8 tháng 6 2023
gọi thời gian dự định đi là `x(h)(x>0)`
Độ dài quãng đg là `60x(km)`
Vì ban đàu xe chạy với vận tốc 60km/h và đi đc nửa đg nên t/g đi trên quãng đg này là `x/2(h)` => t/g đi trên quãng còn lại cx là `x/2(h)` nên
+) độ dài quãng đg xe đi lúc đầu là :`60*x/2 = 30x(km)`
+) độ dài quãng hẹp và xấu xe đi lúc sau là`40*x/2 =20x(km)`
Theo đề bài ta có pt
`30x+20x+40=60x`
`40 = 60x-30x-20x =10x`
`=> x=4(h)`
Khoảng cách từ A đến điểm dừng
`60*4=240(km)`
Xe xuất phát lúc
`11-4=7(h)`