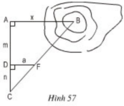
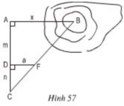
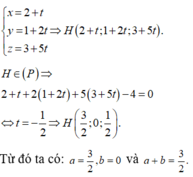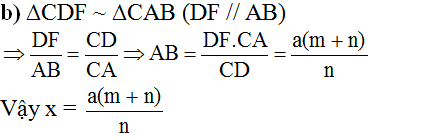Tính khoảng Cách 2 điểm A ,B trong hình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
b) ΔCDF 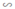 ΔCAB (do DF // AB)
ΔCAB (do DF // AB)
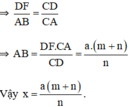

a) Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
b) ΔCDF 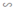 ΔCAB (do DF // AB)
ΔCAB (do DF // AB)
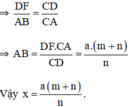

a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow AB \bot \left( {SA{\rm{D}}} \right)\\ \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\end{array}\)
b) Kẻ \(AH \bot SC \Rightarrow d\left( {A,SC} \right) = AH\)
Tam giác \(ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
Tam giác \(SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)
Tam giác \(SAC\) vuông tại \(A\) có đường cao \(AH\)\( \Rightarrow AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\)
Vậy \(d\left( {A,SC} \right) = \frac{{a\sqrt 6 }}{3}\).

Đáp án A
Để hàm số đồng biến trên khoảng 2 ; + ∞ thì
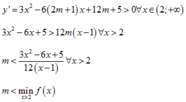
Xét f x = 3 x 2 − 6 x + 5 12 x − 1 có đạo hàm f ' x = 3 x 2 − 6 x + 1 12 x − 1 2 > 0 x > 2
Do đó f(x) đồng biến trên khoảng 2 ; + ∞ hay M i n f x = f 2 = 5 12 ⇒ m < 5 12
Lại có m ∈ − 2017 ; 2017 m ∈ ℤ .
Suy ra có 2018 giá trị của m thỏa mãn

Đáp án C
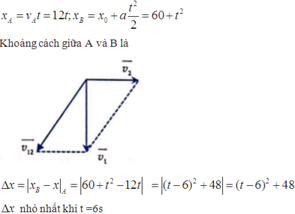
Chọn chiều dương của trục Ox cùng hướng chuyển động của A và B, gốc O tại vị trí ban đầu của A. Gốc thời gian là A và B bắt đầu chuyển động.

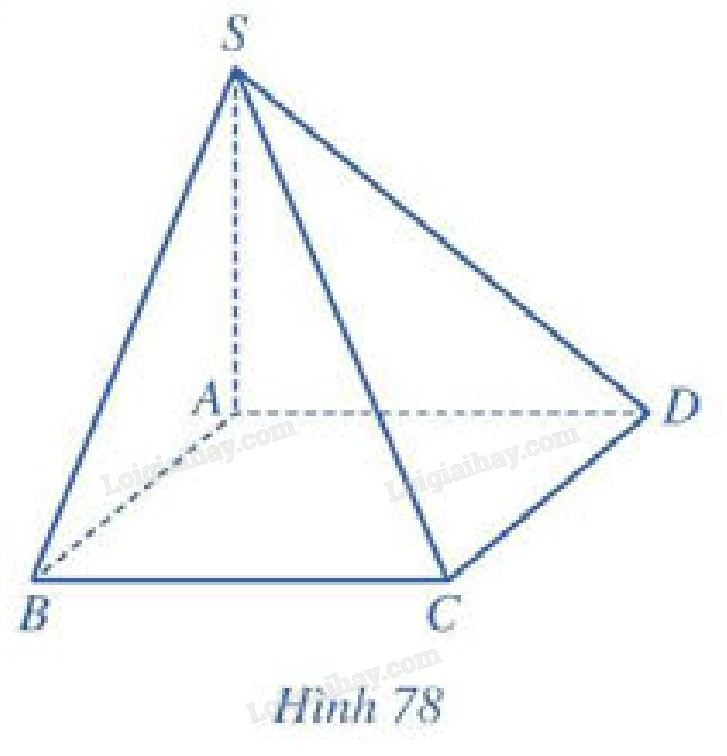
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).

Chọn D
Ta có x + my + (2m + 1)z – m – 2 = 0 <=> m(y + 2z -1) + x + z - 2 = 0 (*)
Phương trình (*) có nghiệm với 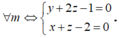
Suy ra (P) luôn đi qua đường thẳng 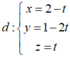
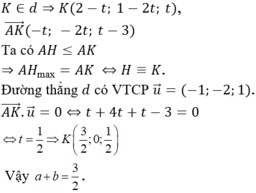

a) Cách đo:
- Chọn thêm hai điểm D và C sao cho A, D, C thẳng hàng và AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thẳng hàng và DF ⊥ AC.
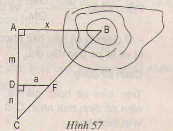
Giải:
a) Cách đo: Chọn thêm hai điểm C và D sao cho A,D,C thẳng hàng AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thằng hàng và DF ⊥ AC.
b) ∆CDF ∽ ∆CAB (DF // AB)
=> DFAB=CDCADFAB=CDCA = > AB = DF.CACD=a(m+n)mDF.CACD=a(m+n)m
vẫy x= DF.CACD=a(m+n)mDF.CACD=a(m+n)m