tg ABC vuông tại A .H là tđ BC, kẻ HM vuông góc AB,HN vuông góc AC a) tg AMHN là hcn b) Kẻ K đối xứng vs H qua N tg AHCK là hình j vì sao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 10 2023
a: Xét tứ giác AMKN có
\(\widehat{AMK}=\widehat{ANK}=\widehat{MAN}=90^0\)
=>AMKN là hình chữ nhật
b: Xét ΔABC có
K là trung điểm của BC
KM//AC
Do đó: M là trung điểm của AB
Xét ΔABC có
K là trung điểm của BC
KN//AB
Do đó: N là trung điểm của AC
Xét tứ giác AKBE có
M là trung điểm chung của AB và KE
nên AKBE là hình bình hành
Xét hình bình hành AKBE có AB\(\perp\)KE
nên AKBE là hình thoi
c: Xét tứ giác AKCF có
N là trung điểm chung của AC và KF
nên AKCF là hình bình hành
=>CF//AK và CF=AK
AKBE là hình bình hành
=>BE//AK và BE=AK
BE//AK
CF//AK
Do đó: BE=CF
BE=AK
CF=AK
Do đó: BE=CF
9 tháng 1 2023
a: Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
nen AMHN là hìh chữ nhật
b: Xét tứ giácc AHKC có
I là trung điểm chung của AK và HC
nên AHKC là hình bình hành
=>AC//HK
18 tháng 10 2021
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{NAM}=90^0\)
nên AMHN là hình chữ nhật
LH
31 tháng 10 2016
bài 1 hình tự vẽ
ABCD là hcn nên góc B=90
áp dụng pytago => BC=6cm
bài 2 hình lười vẽ => tự vẽ hình
tam giác ABC có d tđ AB, e tđ BC
=> DE là đtb
=> DE // và = 1/2 AC (1)
mà M là trung điểm AC => AM = 1/2 AC (2)
(1) và (2) => DE // và = AM
=> ĐPCM
câu b
có câu a mà để ADEM là hcn thì => góc A=90 độ
<=> tam giác ABC vuông tại A
câu c hình như sai, M di chuyển trên BC, M là tđ của BC rồi mà
bài 3
câu a cm tam giác oab cân O
=> oa=ob
cmtt => oa=oc
=> DPCM
câu b
tam giác oab cân o có ox là đường cao
=> góc aox = góc xob
cmtt => góc aoy= góc yoc
tổng 4 góc đó = góc boc
mà góc xoa + góc aoy =90
=> ...
=> góc boc = 180 độ
=> ĐPcm
bài 4
câu a
admn là hcn ( vì có 3 góc vuông)
câu b
cm dn là đtb
=> n là tđ Ac
có ..
=> adce là hbh
mà ac vuông góc de
=> adce là hình thoi
câu c :V, cm ở câu b rồi kìa
câu d, ko biết cách trình bày nhưng để diều đó xảy ra khi tam giác abc cân tại a
vì bài làm hơi dài nên tôi làm hình như hơi quá tắt thì phải, cái chỗ chám chấm ko hiểu thì nói tôi chỉ cho
LH
1 tháng 11 2016
ở chỗ bài 3
góc box + góc xoa + góc aoy + góc yoc = góc boc
mà góc box = góc xoa và góc aoy = góc yoc
=> 2 ( góc xoa + góc aoy) = góc boc
mà góc xoa + góc aoy = 90
=> 2( góc xoa + góc aoy) = 90 * 2 = góc boc = 180
=> ĐPCM
câu b bài 4
tự cm dn là đường trung bình của tam giác abc
=> n là trung điểm ac
có d đối xứng với e qua n => n là trung điểm de
=> adce là hbh
chỉ vậy thôi nhá
15 tháng 12 2016
b,Xét tam giác ADC co :
CH vuong goc voi AD
DN vuong goc voi AC (DN//BA)
=> AM vuông góc với DC ( đường cao thứ 3 của tam giác ADC)
=> dpcm
15 tháng 12 2016
a, Xet tam giac BHA va tam giac DHM co H=90 :
AH=HD
goc BAH = goc MDH (slt)
=> 2 tam giác bằng nhau
=> BA=DM
Ma BA//DM
=> tu giac BDMA la HBH
Ma AD cat BM bang 90
=> BDMA la hinh thoi
b, câu b chờ tí nha
4 tháng 1 2022
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
Do đó: AMHN là hình chữ nhật
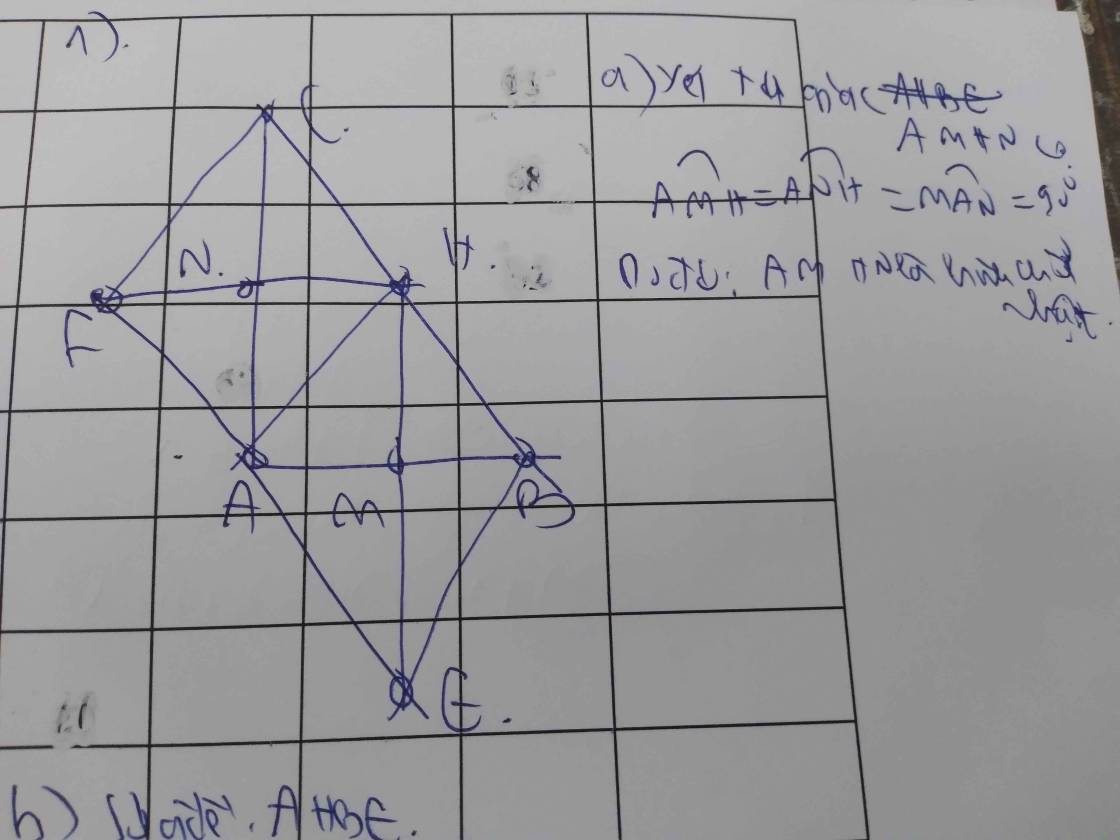
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
Do đó: AMHN là hình chữ nhật
b: Xét ΔABC có
H là trung điểm của BC
HN//AB
Do đó: N là trung điểm của AC
Xét tứ giác AHCK có
N là trung điểm chung của AC và HK
nên AHCK là hình bình hành
mà AC\(\perp\)HK
nên AHCK là hình thoi