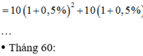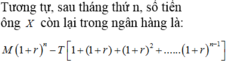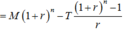Một học sinh A lên kế hoạch tiết kiệm tiền để gửi đi làm từ thiện cho trẻ em vùng cao bằng cáchgửi ngân hàng với lãi suất không đổi 0.7% / tháng. Ban đầu, học sinh A có 1 triệu gửi ngân hàng từ đầu th...

-Theo đề bài, ta có: \(\left\{{}\begin{matrix}u_1=2.10^6\left(đồng\right)\\u_{n+1}=\left(100\%+0,6\%\right)u_n+10^5=1,006u_n+10^5\left(1\right)\end{matrix}\right.\)

(NHÁP:

-Ta sẽ tạo ra dãy cấp số nhân có liên hệ với (1). Để làm vậy, trước tiên đặt \(v_n=u_n-a\Rightarrow u_n=v_n+a\) (a là hằng số).

Khi đó \(v_{n+1}+a=1,006\left(v_n+a\right)+10^5\)

\(\Rightarrow v_{n+1}=1,006v_n+\left(1,006a-a+10^5\right)\)

Để tạo thành cấp số nhân, \(1,006a-a+10^5=0\), giải ra ta được: \(a=\dfrac{-5.10^7}{3}\))

*Đặt \(v_n=u_n+\dfrac{5.10^7}{3}\Rightarrow u_n=v_n-\dfrac{5.10^7}{3}\). Thế vào (1) ta được:

\(v_{n+1}=1,006v_n\) => \(\left(v_n\right)\) là cấp số nhân với \(q=1,006\)

Ta lại có: \(v_1=u_1+\dfrac{5.10^7}{3}=2.10^6+\dfrac{5.10^7}{3}\)

\(\Rightarrow v_n=\left(2.10^6+\dfrac{5.10^7}{3}\right).1,006^{n-1}\)

\(\Rightarrow u_n=\left(2.10^6+\dfrac{5.10^7}{3}\right).1,006^{n-1}-\dfrac{5.10^7}{3}\)

Vậy sau 12 tháng sinh viên A có:

\(u_{12}=\left(2.10^6+\dfrac{5.10^7}{3}\right).1,006^{11}-\dfrac{5.10^7}{3}=3.269.633,331\left(đồng\right)\)

Đúng(1)

PT

Pham Trong Bach

11 tháng 11 2017

Một người lập kế hoạch gửi tiết kiệm ngân hàng như sau: Đầu tháng 1 năm 2019, người đó gửi 10 triệu đồng; sau mỗi đầu tháng tiếp theo, người đó gửi số tiền nhiều hơn 10% so với số tiền đã gửi ở tháng liền trước đó. Biết rằng lãi suất ngân hàng không đổi là 0,5% mỗi tháng và được tính theo hình thức lãi kép. Với kế hoạch như vậy, đến hết tháng 12 năm 2020, số tiền của...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

11 tháng 11 2017

Đáp án A.

Gọi B là số tiền của người đó trong tài khoản tiết kiệm đến hết tháng 12 năm 2020. Khi đó n = 24

Đúng(0)

PT

Pham Trong Bach

21 tháng 1 2018

Đầu mỗi tháng bác An gửi tiết kiệm vào ngân hàng HD Bank một số tiền như nhau với lãi suất 0,45%/tháng. Giả sử rằng lãi suất hàng tháng không thay đổi trong 3 năm liền kể từ khi bác An gửi tiết kiệm. Hỏi bác An cần gửi một lượng tiền tối thiểu T (đồng) bằng bao nhiêu vào ngân hàng HD Bank để sau 3 năm gửi tiết kiệm số tiền lãi đủ để mua được chiếc xe máy có trị giá 30 triệu...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

21 tháng 1 2018

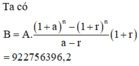
Đáp án C.

Giả sử bác An gửi số tiền tối thiểu hàng tháng là T (đồng). Đặt r = 0,45%.

Hết tháng thứ nhất bác An nhận được số tiền cả gốc và lãi là

T 1 = T + T . r = T . 1 + r .

Hết tháng thứ hai bác An nhận được số tiền cả gốc và lãi là

T 2 = T . 2 + r + T . 2 + r . r = T . r + 1 2 + r + 1 .

Bằng phương pháp quy nạp toán học, ta chứng minh được rằng sau n tháng gửi tiết kiệm thì bác An nhận được số tiền cả gốc và lãi là

T n = T 1 + r n + 1 + r n − 1 + ... + 1 + r .

Dễ dàng tính được T n = T r . 1 + r . 1 + r n − 1 .

Suy ra số tiền lãi sau n tháng gửi tiết kiệm là

L n = T n − T n = T r . 1 + r . 1 + r n − 1 − T n .

Theo giả thiết, ta có n = 36 , L 36 ≥ 30 000 000. Suy ra T ≥ 9 493 000.

Phân tích phương án nhiễu.

Phương án A: Sai do HS tính chỉ gửi 35 tháng.

Phương án B: Sai do HS sử dụng công thức của bài toán tính lãi kép và hiểu đề bài yêu cầu số tiền thu được sau 3 năm đủ để mua xe máy có trị giá 30 triệu đồng nên tìm được T = 25 523 000.

Phương án C: Sai do HS giải đúng như trên nhưng lại làm tròn T = 9 492 000.

Đúng(0)

PT

Pham Trong Bach

1 tháng 11 2018

Đầu mỗi tháng bác An gửi tiết kiệm vào ngân hàng HD Bank một số tiền như nhau với lãi suất 0,45%/tháng. Giả sử rằng lãi suất hàng tháng không thay đổi trong 3 năm liền kể từ khi bác An gửi tiết kiệm. Hỏi bác An cần gửi một lượng tiền tối thiểu T (đồng) bằng bao nhiêu vào ngân hàng HD Bank để sau 3 năm gửi tiết kiệm số tiền lãi đủ để mua được chiếc xe máy có trị giá 30 triệu...

Đọc tiếp

#Mẫu giáo

1