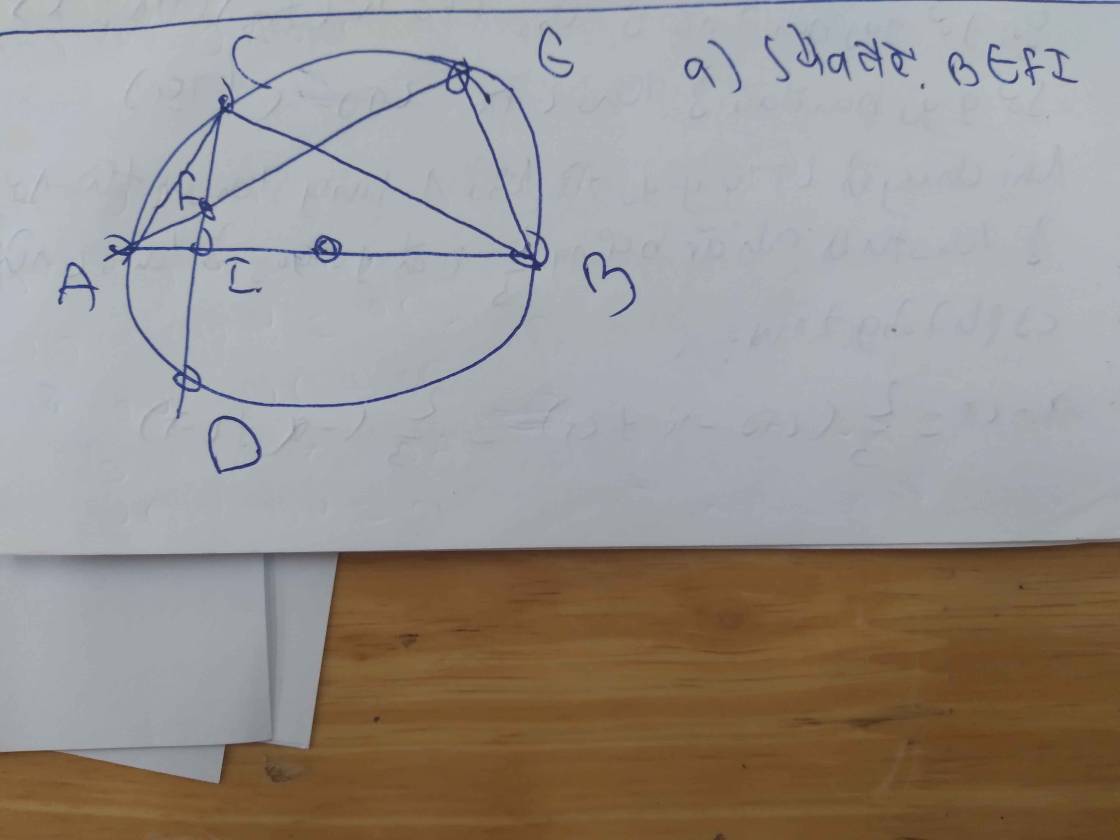
Bài 5 (3,5 điểm)Cho đường tròn (O) đường kính BC = 2R và dây cung AB = R
a) Chứng minh AABC vuông tại A. Tính độ dài cạnh AC theo R.
b) Trên tia OA lấy điểm D sao cho A là trung điểm của OD. Chứng minh DB là tiếp tuyển của đường tròn (O).
c) Vẽ tiếp tuyến DM với đường tròn (O) (M là tiếp điểm). Chứng minh ABDM là tam giác đều.
d) Chứng minh tứ giác AMOB là hình thoi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó; ΔABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=R\sqrt{3}\)
b: Xét ΔDOB có
BA là đường trung tuyến
BA=DO/2
Do đó: ΔDOB vuông tại B
hay DB là tiếp tuyến của (O)

bạn tự vẽ hình nha
bạn dễ dàng chứng minh đc tam giác ACO là tam giác đều ( AM = MO ; CM vuong goc vs AO )
trong tam giác ECO có EA = AO = AC nên suy ra tam giac ECO vuong tai C
suy ra EC vuong goc vs OC . (dpcm )
b, sử dụng định lí pitago

a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=\left(2R\right)^2-R^2=3R^2\)
=>\(AC=R\sqrt{3}\)
b: Ta có: ΔOAC cân tại O
mà OE là đường trung tuyến
nên OE là phân giác của góc AOC
=>OF là phân giác của góc AOC
Xét ΔOCF và ΔOAF có
OC=OA
\(\widehat{COF}=\widehat{AOF}\)
OF chung
Do đó: ΔOCF=ΔOAF
=>\(\widehat{OAF}=\widehat{OCF}=90^0\)
=>FA là tiếp tuyến của (O)

a: BA là tiếp tuyến của (O) có B là tiếp điểm
=>OB\(\perp\)BA tại B
=>ΔOBA vuông tại B
ΔBOA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
b: ΔOBC cân tại O
mà OA là đường cao
nên OA là tia phân giác của \(\widehat{BOC}\)
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OCA}=\widehat{OBA}=90^0\)
=>AC là tiếp tuyến của (O)
c: Xét ΔABO vuông tại B có \(sinBAO=\dfrac{BO}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
ΔOBA=ΔOCA
=>\(\widehat{BAO}=\widehat{CAO}\) và AB=AC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=2\cdot30^0=60^0\)
Xét ΔABC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔABC đều