Tìm abcd sao cho \(\sqrt[6]{4abcd}\)thuộc N
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2015
\(\frac{1}{\sqrt{4}+\sqrt{5}}+\frac{1}{\sqrt{5}+\sqrt{6}}+...+\frac{1}{\sqrt{n}+\sqrt{n+1}}=10\)
\(\frac{\sqrt{4}-\sqrt{5}}{\left(\sqrt{4}+\sqrt{5}\right)\left(\sqrt{4}-\sqrt{5}\right)}+\frac{\sqrt{5}-\sqrt{6}}{\left(\sqrt{5}+\sqrt{6}\right)\left(\sqrt{5}-\sqrt{6}\right)}+...+\frac{\sqrt{n}-\sqrt{n+1}}{\left(\sqrt{n}+\sqrt{n+1}\right)\left(\sqrt{n}-\sqrt{n+1}\right)}=10\)
\(\frac{\sqrt{4}-\sqrt{5}}{4-5}+\frac{\sqrt{5}-\sqrt{6}}{5-6}+...+\frac{\sqrt{n}-\sqrt{n+1}}{n-\left(n+1\right)}=10\)
\(\frac{\sqrt{4}-\sqrt{5}}{-1}+\frac{\sqrt{5}-\sqrt{6}}{-1}+...+\frac{\sqrt{n}-\sqrt{n+1}}{-1}=10\)
\(\frac{\sqrt{4}-\sqrt{n+1}}{-1}=10\)
\(2-\sqrt{n+1}=-10\)
\(\sqrt{n+1}=12\)
\(\Rightarrow n+1=144\Rightarrow n=143\)
29 tháng 12 2021
a: \(\overrightarrow{MA}=\left(1-x_M;-1\right)\)
\(\overrightarrow{MB}=\left(3-x_M;0\right)\)
Để ΔMAB vuông tại M thì \(\left(1-x_M\right)\left(3-x_M\right)-1=0\)
=>xM=2
DT
0
19 tháng 9 2016
Ta có \(1\sqrt{\left(6-2\sqrt{5}\right)^n}=\left(\sqrt{5}-1\right)^n\)
\(1\sqrt{\left(6+2\sqrt{5}\right)^n}=\left(\sqrt{5}+1\right)^n\)
Với n = 1 thì VT = \(2\sqrt{5}\ne6\)
Vố n \(\ge2\)thì VT \(\ge12\)
Vậy pt vô nghiệm
TM
26 tháng 6 2023
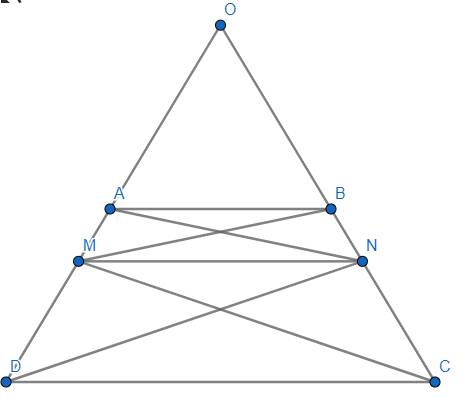
(a) Cho \(AD\cap BC=\left\{O\right\}.\) Do \(AB\left|\right|CD\left(gt\right)\Rightarrow\hat{OAB}=\hat{ODC}=\hat{OCD}=\hat{OBA}\) (đồng vị và tính chất hình thang cân) \(\Rightarrow\Delta OAB\) cân tại \(O\Rightarrow OA=OB.\)
Mà: \(AM=BN\Rightarrow OA+AM=OB+BN\Leftrightarrow OM=ON\Rightarrow\Delta OMN\) cân tại \(O\Rightarrow\hat{OMN}=\hat{ONM}=\dfrac{180^o-\hat{O}}{2}\left(1\right)\).
Lại có \(\Delta OAB\) cân tại \(O\left(cmt\right)\Rightarrow\hat{OAB}=\hat{OBA}=\dfrac{180^o-\hat{O}}{2}\left(2\right)\)
Từ (1) và (2), suy ra: \(\hat{OMN}=\hat{OAB}\Rightarrow AB\left|\right|MN\).
Mà: \(AB\left|\right|CD\left(gt\right)\Rightarrow AB\left|\right|MN\left|\right|CD\left(3\right)\)
Từ (1) và (3) \(\Rightarrow ABNM\) là hình thang cân (đpcm).
Mặt khác: \(\hat{MDC}=\hat{NCD}\left(gt\right)\left(4\right)\)
Từ (3) và (4) \(\Rightarrow MNCD\) là hình thang cân (đpcm).
