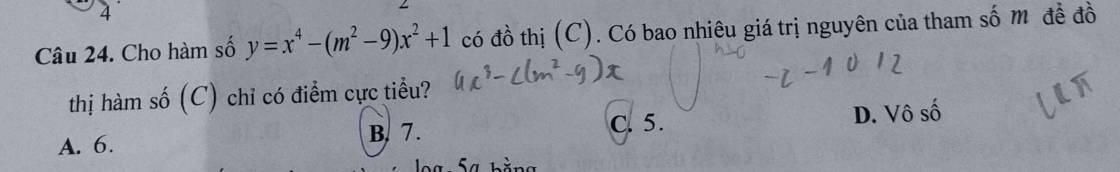Giúp mình câu 24
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 2 2023
Câu 23:
Ta có: nH2O - nCO2 = nA = 0,23 - 0,14 = 0,09 (mol)
\(\Rightarrow\left\{{}\begin{matrix}\%n_A=\dfrac{0,09}{0,1}.100\%=90\%\\\%n_B=10\%\end{matrix}\right.\)
→ Đáp án: A
Câu 24:
nCO2 = nH2O ⇒ X là anken.
→ Đáp án: D
H
2 tháng 2 2023
$Ba(OH)_2 + CO_2 \to BaCO_3 + H_2O$
Theo PTHH :
$n_{CO_2} = n_{BaCO_3} = \dfrac{29,55}{197} = 0,15(mol)$
$m_{H_2O} + m_{CO_2} = 29,55 - 19,35 = 10,2(gam)$
$\Rightarrow n_{H_2O} = 0,2(mol)$
Bảo toàn nguyên tố với C và H :
$n_C = n_{CO_2} = 0,15(mol) ;n_H =2 n_{H_2O} = 0,4 (mol)$
Ta có :
$n_C : n_H = 0,15 : 0,4 = 3 : 8$
Vậy hidrocacbon cần tìm là $C_3H_8$
10 tháng 3 2023
Ta có: mY = m bình tăng = 0,382 (g)
\(n_Z=\dfrac{0,28}{22,4}=0,0125\left(mol\right)\)
\(M_Z=10,08.2=20,16\left(g\right)\)
\(\Rightarrow m_Z=0,0125.20,16=0,252\left(g\right)\)
Mà: mX = mY + mZ = 0,382 + 0,252 = 0,634 (g)
→ Đáp án: D
5 tháng 3 2023
24) \(M_X=17.2=34\left(g/mol\right)\)
Quy đổi \(X\left\{{}\begin{matrix}C_2H_4\\CH_4\\C_3H_4\\C_4H_4\end{matrix}\right.\) thành \(C_{\overline{n}}H_4\)
\(\Rightarrow12\overline{n}+4=34\Leftrightarrow n=2,5\)
BTNT C: \(n_{CaCO_3}=n_{CO_2}=n_C=2,5.n_X=2,5.0,025=0,0625\left(mol\right)\)
BTNT H: \(n_{H_2O}=2n_X=0,05\left(mol\right)\)
\(\Rightarrow\Delta m_{\uparrow}=0,0625.44+0,05.18=3,65\left(g\right)\)
Chọn C
5 tháng 3 2023
Đặt CTTQ X: \(C_{\overline{n}}H_4\)
\(M_X=17.2=34\) \((g/mol)\)
\(\Rightarrow12\overline{n}+4=34\)
\(\Rightarrow\overline{n}=2,5\)
`->` CTTQ X có dạng: \(C_{2,5}H_4\)
\(C_{2,5}H_4+3,5O_2\rightarrow\left(t^o\right)2,5CO_2+2H_2O\)
0,025 0,0625 0,05 ( mol )
\(m_{bình.tăng}=m_{CO_2}+m_{H_2O}\)
\(=0,0625.44+0,05.18=3,65\left(g\right)\)
`->` Chọn C
12 tháng 1 2022
Câu 18: B
Câu 19: B
Câu 20: D
Câu 21; D
Câu 22: B
Câu 23: B
Câu 24: A
27 tháng 6 2023
24:
a: x^2+y^2-2x-4y-4=0
=>x^2-2x+1+y^2-4y+4-9=0
=>(x-1)^2+(y-2)^2=9
=>R=3 và I(1;2)
b: Δ: 3x+4y+1=0
Gọi (d) là phương trình cần tìm
(d)//Δ nên (d): 3x+4y+c=0
R=3; I(1;2)
Vì (d) là tiếp tuyến của (C) nên ta có:
d(I;(d))=R=3
=>\(\dfrac{\left|1\cdot3+2\cdot4+c\right|}{\sqrt{3^2+4^2}}=3\)
=>|c+11|=15
=>c=4 hoặc c=-26
13 tháng 9 2021
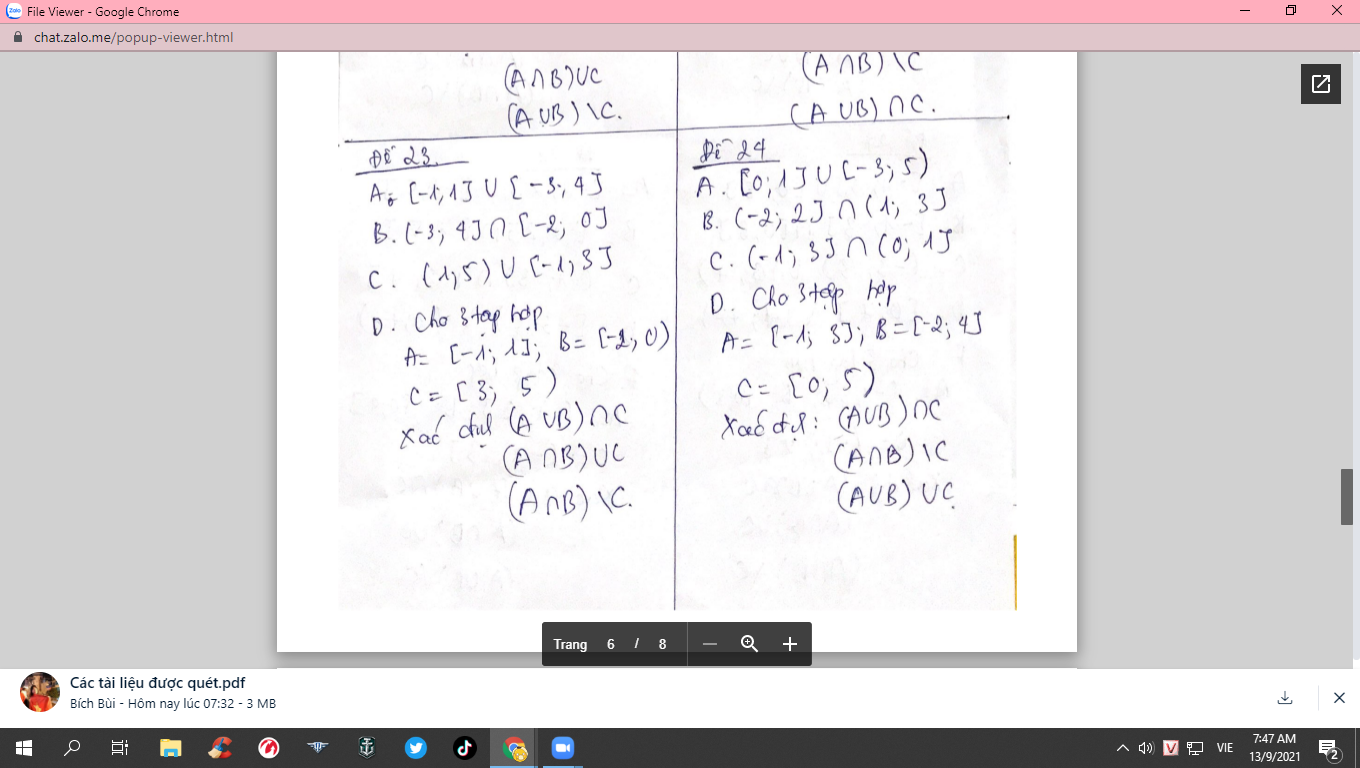
\(a,A=\left\{-3;-2;-1;0;1;2;3;4\right\}\\ b,B=\left\{2\right\}\\ c,C=\left\{1\right\}\\ d,\left(A\cup B\right)\cap C=\left\{0;1;2;3;4\right\}\\ \left(A\cap B\right)\ C=\left\{-1\right\}\\ \left(A\cup B\right)\cup C=\left\{-2;-1;0;1;2;3;4\right\}\)
13 tháng 9 2021
câu \(d,\) ý 2 mình ghi nhầm nha bạn, sửa lại:
\(\left(A\cap B\right)\C=\left\{-1\right\}\)
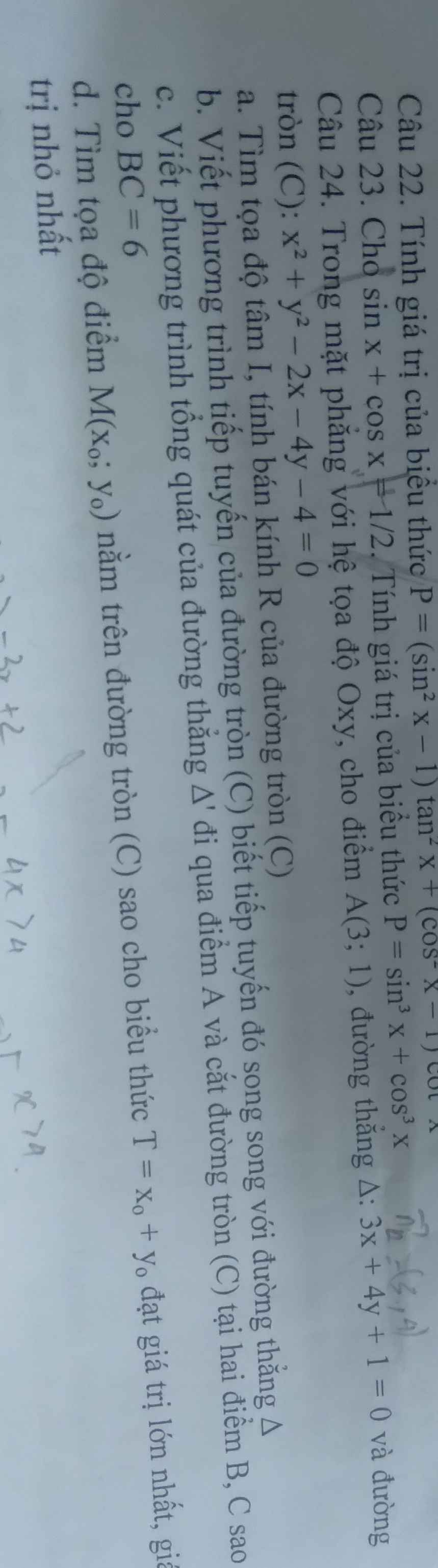
câu 21 22 23 24 giúp mình nha
Lời giải:
Với hệ số lớn nhất là $1>0$ thì hàm trùng phương chỉ có cực tiểu khi mà:
$y'=4x^3-2(m^2-9)x=0$ có 1 nghiệm duy nhất.
$\Leftrightarrow 2x[2x^2-(m^2-9)]=0$ có nghiệm duy nhất. (*)
Mà pt này đã có sẵn nghiệm $x=0$ nên (*) xảy ra khi mà $2x^2-(m^2-9)=0$ vô nghiệm hoặc có nghiệm $x=0$
$\Leftrightarrow m^2-9=0$ hoặc $m^2-9<0$
$\Leftrightarrow m^2\leq 9$
$\Leftrightarrow -3\leq m\leq 3$
$\Leftrightarrow m\in\left\{-3; -2; -1; 0; 1; 2; 3\right\}$
Tức là có 7 giá trị $m$ nguyên tm.