32769 chia 24 ai giup em cau nay voi a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
$x=\frac{3}{4}+\frac{1}{2}=\frac{5}{4}$
b.
$x+\frac{3}{10}=\frac{17}{12}-\frac{17}{20}=\frac{17}{30}$
$x=\frac{17}{30}-\frac{3}{10}=\frac{4}{15}$
c.
$x=\frac{3}{4}-\frac{7}{8}=\frac{-1}{8}$
d.
$\frac{x}{20}=\frac{7}{12}+\frac{11}{30}=\frac{19}{20}$
$\Rightarrow x=19$

Đầu tiên, để 123a chi hết cho 9 thì a=3 mà để 123a không chia hết cho 9 và dư 2 thì a= 3+2=5 Vậy để 123a không chia hết cho 9 và dư 2 thì a=5

A= (357-62)-(-62-643)
=375-62+62+643
=1018
1 đúng nha

Simplifying 5(2x + 1) = 3(x + -2) Reorder the terms: 5(1 + 2x) = 3(x + -2) (1 * 5 + 2x * 5) = 3(x + -2) (5 + 10x) = 3(x + -2) Reorder the terms: 5 + 10x = 3(-2 + x) 5 + 10x = (-2 * 3 + x * 3) 5 + 10x = (-6 + 3x) Solving 5 + 10x = -6 + 3x Solving for variable 'x'. Move all terms containing x to the left, all other terms to the right. Add '-3x' to each side of the equation. 5 + 10x + -3x = -6 + 3x + -3x Combine terms: 10x + -3x = 7x 5 + 7x = -6 + 3x + -3x Combine terms: 3x + -3x = 0 5 + 7x = -6 + 0 5 + 7x = -6 Add '-5' to each side of the equation. 5 + -5 + 7x = -6 + -5 Combine terms: 5 + -5 = 0 0 + 7x = -6 + -5 7x = -6 + -5 Combine terms: -6 + -5 = -11 7x = -11 Divide each side by '7'. x = -1.571428571 Simplifying x = -1.571428571

g: \(\text{Δ}=\left(-6\right)^2-4\left(2m+1\right)=36-8m-4=-8m+32\)
Để phương trình có hai nghiệm thì -8m+32>=0
=>m<=4
Để phương trình có hai nghiệm cùng âm thì:
\(\left\{{}\begin{matrix}m< =4\\\dfrac{-\left(-6\right)}{1}< 0\\2m+1>0\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
h: \(\left\{{}\begin{matrix}2x_1-x_2=15\\x_1+x_2=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=7\\x_2=-1\end{matrix}\right.\)
x1*x2=2m+1
=>2m+1=-7
=>2m=-8
=>m=-4
i: \(x_1^2+x_2^2=5\)
=>(x1+x2)^2-2x1x2=5
=>6^2-2(2m+1)=5
=>36-4m-2=5
=>34-4m=5
=>4m=29
=>m=29/4(loại)
j: \(x_1^3+x_2^3=5\)
=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=5\)
=>\(6^3-3\cdot6\cdot\left(2m+1\right)=5\)
=>216-18(2m+1)=5
=>18(2m+1)=211
=>2m+1=211/18
=>2m=193/18
=>m=193/36(loại)

A=P^2-P
\(=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-2\right)^2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
\(=\dfrac{x+2\sqrt{x}+1-x+\sqrt{x}+2}{\left(\sqrt{x}-2\right)^2}=\dfrac{3\sqrt{x}+3}{\left(\sqrt{x}-2\right)^2}>=0\)
=>P^2>=P
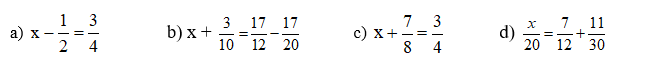
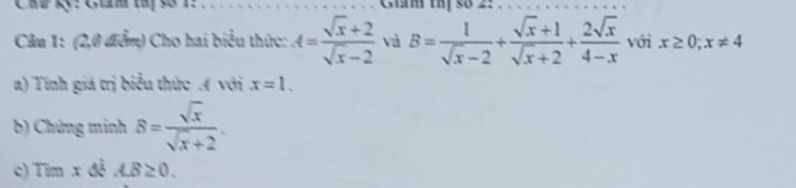


 giup minh cau nay voi a
giup minh cau nay voi a
1365.375 ra số dư á bn